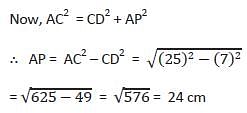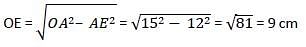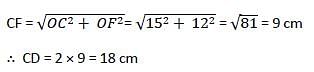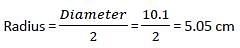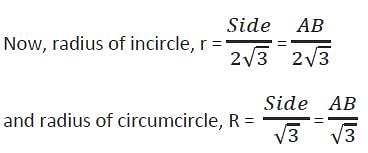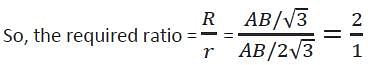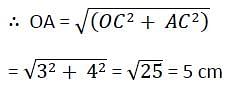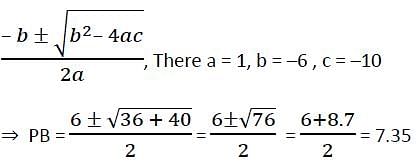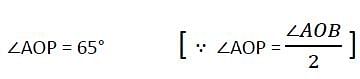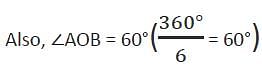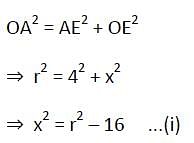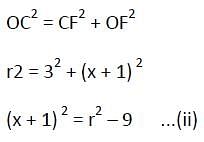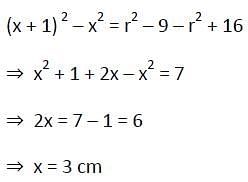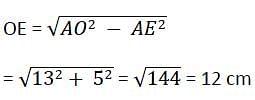MCQ: Circles - 1 - SSC CGL MCQ
15 Questions MCQ Test Quantitative Aptitude for SSC CGL - MCQ: Circles - 1
Directions: Kindly study the following questions carefully and choose the right answer:
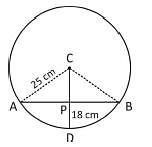
The diameter of a circle with centre at C is 50 cm. CP is a radial segment of thecircle. AB is a chord perpendicular to CP and passes through P. CP producedintersects the circle at D. If DP = 18 cm, then what is the length of AB?
Directions: Kindly study the following questions carefully and choose the right answer:
Two equal circles of radius 4 cm intersect each other such that each passes through the centre of the other. The length of the common chord is :
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Directions: Kindly study the following question carefully and choose the right answer:
Two parallel chords are drawn in a circle of diameter 30 cm. The length of one chord is 24 cm and the distance between the two chords is 21 cm. The length of the other chord is
Directions: Kindly study the following question carefully and choose the right answer:
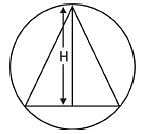
A circle of radius 10 cm has an equilateral triangle inscrisbed in it. the length of the perpendicular drawn from the centre to any side of the triangle is
Directions: Kindly study the following question carefully and choose the right answer:
The largest chord of a circle is known to be 10.1 cm. The radius of this circle must be :
Directions: Kindly study the following question carefully and choose the right answer:
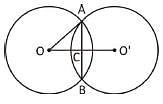
If two equal circles whose centres are O and O', intersect each other at the point A and B, OO' = 12 cm and AB = 16 cm, then the radius of the circle is
Directions: Kindly study the following question carefully and choose the right answer:
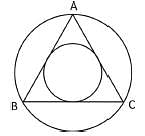
In a ΔABC, AB = BC = CA. The ratio of the radius of the circumcircle to that of the incircle is
Directions: Kindly study the following question carefully and choose the right answer:
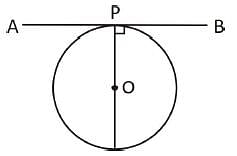
The length of the chord of a circle is 8 cm and perpendicular distance between centre and the chord is 3 cm. Then the radius of the circle is equal to :
Directions: Kindly study the following question carefully and choose the right answer:
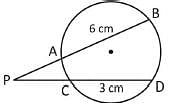
Chords AB and CD of a circle intersect externally at P. If AB = 6 cm, CD = 3 cm and PD = 5 cm, then the length of PB is
Directions: Kindly study the following question carefully and choose the right answer:
Consider the following statements
I. The tangent of a circle is a line that meets the circle in one and only one point.
II. The tangent of a circle at the end point of the diameter is perpendicular to the diameter.
Which of the above statements is/are correct?
Directions: Kindly study the following question carefully and choose the right answer:
The length of a chord of a circle is equal to the radius of the circle. The angle which this chord subtends in the major segment of the circle is equal to
Directions: Kindly study the following question carefully and choose the right answer:
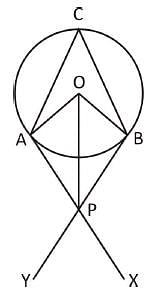
A circle (with centre at O) is touching two intersecting lines AX and BY. The two points of contact A and B subtend an angle of 65° at any point C on the circumference of the circle. If P is the point of intersection of the two lines, then the measure of ∠APO is
Directions: Kindly study the following question carefully and choose the right answer:
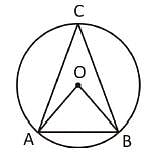
A regular hexagon is inscrisbed in a circle of radius 5 cm. If x is the area inside the circle but outside the regular hexagon, then which one of the following is correct?
Directions: Kindly study the following question carefully and choose the right answer:
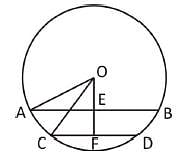
AB = 8 cm and CD = 6 cm are two parallel chords on the same side of the centre of a circle. The distance between them is 1 cm. The radius of the circle is
Directions: Kindly study the following question carefully and choose the right answer:
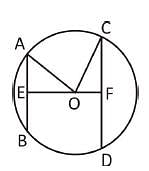
AB and CD are two parallel chords on the opposite sides of the centre of the circle. If AB = 10 cm, CD = 24 cm and the radius of the circle is 13 cm, the distance between the chords is
|
314 videos|170 docs|185 tests
|
|
314 videos|170 docs|185 tests
|