Test: Continuous Time Signal Analysis - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test Digital Signal Processing - Test: Continuous Time Signal Analysis
The Fourier series representation of any signal x(t) is defined as:
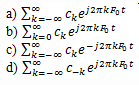
Which of the following is the equation for the Fourier series coefficient?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Which of the following is a Dirichlet condition with respect to the signal x(t)?
Which of the following is the Fourier series representation of the signal x(t)?
d) None of the mentioned
The equationis the representation of Fourier series.
What is the spectrum that is obtained when we plot |ck |2 as a function of frequencies kF0, k=0,±1,±2..?
What is the spectrum that is obtained when we plot |ck| as a function of frequency?
What is the equation of the Fourier series coefficient ck of an non-periodic signal?
Which of the following relation is correct between Fourier transform X(F) and Fourier series coefficient ck?
|
3 videos|50 docs|54 tests
|
|
3 videos|50 docs|54 tests
|

















