Test: Discrete Time System Analysis - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test Digital Signal Processing - Test: Discrete Time System Analysis
Resolve the sequence 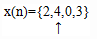 into a sum of weighted impulse sequences
into a sum of weighted impulse sequences
The formula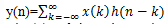 that gives the response y(n) of the LTI system as the function of the input signal x(n) and the unit sample response h(n) is known as:
that gives the response y(n) of the LTI system as the function of the input signal x(n) and the unit sample response h(n) is known as:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
What is the order of the four operations that are needed to be done on h(k) in order to convolute x(k) and h(k)?
Step-1:Folding
Step-2:Multiplicaton with x(k)
Step-3:Shifting
Step-4:Summation
Step-1:Folding
Step-2:Multiplicaton with x(k)
Step-3:Shifting
Step-4:Summation
The impulse response of a LTI system is h(n)={1,1,1}. What is the response of the signal to the input x(n)={1,2,3}?
Determine the output y(n) of a LTI system with impulse response h(n)=anu(n),|a|<1with the input sequence x(n)=u(n).
Determine the impulse response for the cascade of two LTI systems having impulse responses h1(n)=(1/2)2 u(n) and h2(n)= (1/4)2 u(n).
An LTI system is said to be causal if and only if
|
3 videos|50 docs|54 tests
|
|
3 videos|50 docs|54 tests
|

















