All Courses
Get the App Signup / Login
Sign in Open App
Electronics and Communication Engineering (ECE) Exam  >  Electronics and Communication Engineering (ECE) Tests  >  Digital Signal Processing  >  Test: Discrete Time Systems - Electronics and Communication Engineering (ECE) MCQ

Test: Discrete Time Systems - Electronics and Communication Engineering (ECE) MCQ


Test Description

10 Questions MCQ Test Digital Signal Processing - Test: Discrete Time Systems

Test: Discrete Time Systems for Electronics and Communication Engineering (ECE) 2024 is part of Digital Signal Processing preparation. The Test: Discrete Time Systems questions and answers have been prepared according to the Electronics and Communication Engineering (ECE) exam syllabus.The Test: Discrete Time Systems MCQs are made for Electronics and Communication Engineering (ECE) 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Discrete Time Systems below.
Solutions of Test: Discrete Time Systems questions in English are available as part of our Digital Signal Processing for Electronics and Communication Engineering (ECE) & Test: Discrete Time Systems solutions in Hindi for Digital Signal Processing course. Download more important topics, notes, lectures and mock test series for Electronics and Communication Engineering (ECE) Exam by signing up for free. Attempt Test: Discrete Time Systems | 10 questions in 10 minutes | Mock test for Electronics and Communication Engineering (ECE) preparation | Free important questions MCQ to study Digital Signal Processing for Electronics and Communication Engineering (ECE) Exam | Download free PDF with solutions
Test: Discrete Time Systems - Question 1
Save

The output signal when a signal x(n)=(0,1,2,3) is processed through an ‘Identical’ system is:

Detailed Solution for Test: Discrete Time Systems - Question 1

Explanation: An identical system is a system whose output is same as the input, that is it does not perform any operation on the input and transmits it.

Test: Discrete Time Systems - Question 2
Save

If a signal x(n) is passed through a system to get an output signal of y(n)=x(n+1), then the signal is said to be:

Detailed Solution for Test: Discrete Time Systems - Question 2

Explanation: For example, the value of the output at the time n=0 is y(0)=x(1), that is the system is advanced by one unit.

1 Crore+ students have signed up on EduRev. Have you? Download the App
Test: Discrete Time Systems - Question 3
Save

 If the output of the system is 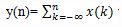with an input of x(n) then the system will work as:

Detailed Solution for Test: Discrete Time Systems - Question 3

Explanation: From the equation given, y(n)=x(n)+x(n-1)+x(n-2)+…. .This system calculates the running sum of all the past input values till the present time. So, it acts as an accumulator.

Test: Discrete Time Systems - Question 4
Save

The block denoted as follows is known as:
Detailed Solution for Test: Discrete Time Systems - Question 4

Explanation: If the function to this block is x(n) then the output from the block will be x(n-1). So, the block is called as delay block or delay element.

Test: Discrete Time Systems - Question 5
Save

 The output signal when a signal x(n)=(0,1,2,3) is processed through an ‘Delay’ system is:
Detailed Solution for Test: Discrete Time Systems - Question 5

Explanation: An delay system is a system whose output is same as the input, but after a delay.

Test: Discrete Time Systems - Question 6
Save

 The system described by the input-output equation y(n)=nx(n)+bx3(n) is a: 
Detailed Solution for Test: Discrete Time Systems - Question 6

Explanation: Since the output of the system y(n) depends only on the present value of the input x(n) but not on the past or the future values of the input, the system is called as static or memory-less system.

Test: Discrete Time Systems - Question 7
Save

Whether the system described by the input-output equations y(n)=x(n)-x(n-1) a Time-variant system? 
Detailed Solution for Test: Discrete Time Systems - Question 7

Explanation: If the input is delayed by k units then the output will be y(n,k)=x(n-k)-x(n-k-1)
If the output is delayed by k units then y(n-k)=x(n-k)-x((n-k)-1)
=>y(n,k)=y(n-k). Hence the system is time-invariant.

Test: Discrete Time Systems - Question 8
Save

 The system described by the input-output equations y(n)=x2(n) is a Non-linear system.
Detailed Solution for Test: Discrete Time Systems - Question 8

Explanation: Given equation is y(n)=x2(n)
Let y1(n)=x12(n) and y2(n)=x22(n)
y3(n)=y1(n)+y2(n)= x12(n)+ x22(n)≠(x1(n)+x2(n))2
So the system is non-linear.

Test: Discrete Time Systems - Question 9
Save

If the output of the system of the system at any ‘n’ depends only the present or the past values of the inputs then the system is said to be:
Detailed Solution for Test: Discrete Time Systems - Question 9

Explanation: A system is said to be causal if the output of the system is defined as the function shown below
y(n)=F[x(n),x(n-1),x(n-2),…] So, according to the conditions given in the question, the system is a causal system.

Test: Discrete Time Systems - Question 10
Save

 If a system do not have a bounded output for bounded input, then the system is said to be:
Detailed Solution for Test: Discrete Time Systems - Question 10

Explanation: An arbitrary relaxed system is said to be BIBO stable if it has a bounded output for every value in the bounded input. So, the system given in the question is a Non-stable system.

3 videos|50 docs|54 tests
Join Course
Information about Test: Discrete Time Systems Page
In this test you can find the Exam questions for Test: Discrete Time Systems solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Discrete Time Systems, EduRev gives you an ample number of Online tests for practice

Top Courses for Electronics and Communication Engineering (ECE)

3 videos|50 docs|54 tests
Join Course
Download as PDF

Top Courses for Electronics and Communication Engineering (ECE)

Important Questions for Discrete Time Systems

Find all the important questions for Discrete Time Systems at EduRev.Get fully prepared for Discrete Time Systems with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Discrete Time Systems syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Discrete Time Systems resources.

Discrete Time Systems MCQs with Answers

Prepare for the Discrete Time Systems within the Electronics and Communication Engineering (ECE) exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Discrete Time Systems Digital Signal Processing

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Discrete Time Systems with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup