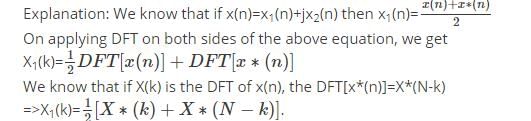Test: FFT Algorithms Applications - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test Digital Signal Processing - Test: FFT Algorithms Applications
FFT algorithm is designed to perform complex operations.
If x1(n) and x2(n) are two real valued sequences of length N, and let x(n) be a complex valued sequence defined as x(n)=x1(n)+jx2(n), 0≤ n≤ N-1, then what is the value of x2(n)?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If X(k) is the DFT of x(n) which is defined as x(n)=x1(n)+jx2(n), 0≤ n≤ N-1, then what is the DFT of x1(n)?
If X(k) is the DFT of x(n) which is defined as x(n)=x1(n)+jx2(n), 0≤ n≤ N-1, then what is the DFT of x1(n)?
If g(n) is a real valued sequence of 2N points and x1(n)=g(2n) and x2(n)=g(2n+1), then what is the value of G(k), k=0,1,2…N-1?
If g(n) is a real valued sequence of 2N points and x1(n)=g(2n) and x2(n)=g(2n+1), then what is the value of G(k), k=N,N-1,…2N-1?
Decimation-in frequency FFT algorithm is used to compute H(k).
How many complex multiplications are need to be performed for each FFT algorithm?
How many complex additions are required to be performed in linear filtering of a sequence using FFT algorithm?
How many complex multiplication are required per output data point?
|
3 videos|50 docs|54 tests
|
|
3 videos|50 docs|54 tests
|