Test: FIR System Structures - 2 - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test Digital Signal Processing - Test: FIR System Structures - 2
Which of the following is the application of lattice filter?
If we consider a sequence of FIR filer with system function Hm(z)=Am(z), then what is the definition of the polynomial Am(z)?
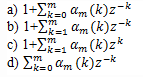
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
What is the unit sample response of the mth filter?
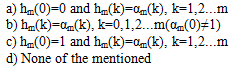
The FIR filter whose direct form structure is as shown below is a prediction error filter.
What is the output of the single stage lattice filter if x(n) is the input?
What is the output from the second stage lattice filter when two single stage lattice filers are cascaded with an input of x(n)?
What is the value of the coefficient α2(1) in the case of FIR filter represented in direct form structure with m=2 in terms of K1 and K2?
The constants K1 and K2 of the lattice structure are called as reflection coefficients.
If a three stage lattice filter with coefficients K1=1/4, K2=1/2 K3=1/3, then what are the FIR filter coefficients for the direct form structure?
What are the lattice coefficients corresponding to the FIR filter with system function H(z)= 1+(13/24)z-1+(5/8)z-2+(1/3)z-3?
|
3 videos|50 docs|54 tests
|
|
3 videos|50 docs|54 tests
|

















