Test: Relative Velocity in Two Dimensions - NEET MCQ
10 Questions MCQ Test Physics Class 11 - Test: Relative Velocity in Two Dimensions
A boat sails across a river with a velocity of 10 km/hr. If resultant boat velocity is 14 km/hr, then what is the velocity of river water?
The angular speed of the earth about its own axis is:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Rain is falling vertically with the speed of 30 m/s. A man rides a bicycle with the speed of 10 m/s in east to west direction. What is the direction in which he should hold the umbrella?
The angular speed of a wheel of radius 0.50 m moving with the speed of 20 m/s is:
In 5 seconds a body covers a distance of 50 m and in 10 seconds it covers 80 m with uniform acceleration. What is the distance traveled in 15 seconds?
The angular speed of a flywheel making 210 revolutions per minute is:
A boat is moving with a velocity  with respect to the ground. The water in the river is moving with a velocity
with respect to the ground. The water in the river is moving with a velocity 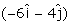 with respect to the ground. What is the relative velocity of boat with respect to river?
with respect to the ground. What is the relative velocity of boat with respect to river?
The angular speed of the second hand of a watch is :
A monkey is running on the ground, next to a train, in the direction of the train. The speed of the monkey is 5km/h and the speed of the train is 100km/h. What is the velocity of the monkey with respect to the train?
The angular speed of a wheel of radius 0.50 m moving with the speed of 20 m/s is:
|
102 videos|411 docs|121 tests
|



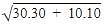 at an angle of tan-1 ⅓
at an angle of tan-1 ⅓