Test: K-Map - 1 - Electrical Engineering (EE) MCQ
10 Questions MCQ Test Analog and Digital Electronics - Test: K-Map - 1
Minimize the following expression using k-Map
Y = ∑m (0,1,5,9,13,14,15) + d (3,4,7,10,11)
Y = ∑m (0,1,5,9,13,14,15) + d (3,4,7,10,11)
The minimized sum of products expression for f(a,b,c,d) = Ʃm(0,1,5,6,7,8,9) with don’t care Ʃm(10,11,12,13,14,15) is ___________.
There are 4 variables in the Boolean function and the value of the function is 1. Find the number of cells in the K-Map which will contain a 1 when SOP expression is used.
The simplification in minimal sum of product (SOP) of Y = F(A, B, C, D) = ∑m (0, 2, 3, 6, 7) + ∑d (8, 10, 11, 15) using K-maps is
Digital input signals A, B, C with A as the MSB and C as the LSB are used to realize the Boolean function F = m0 + m2 + m3 + m5 + m7, where mi denotes the ith minterm. In addition, F has a don’t care for m1. The simplified expression for F is given by:
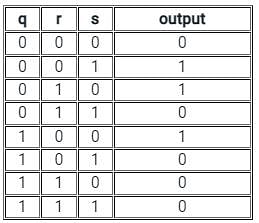
A problem detector system produces an alarm in the factory when one of the three conditions occurs. The system is designed as such tha only one condition can occur at a time. If the three conditions are defined as q, r, and s respectively, the output logic for the system is given as
Consider the following sum of products expression, F

The equivalent product of sums expression is
|
137 videos|144 docs|71 tests
|


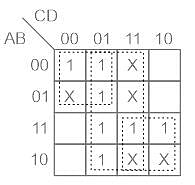



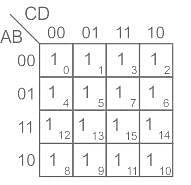




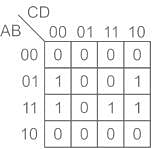
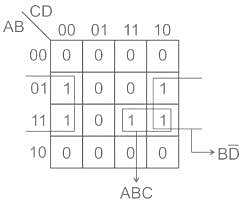
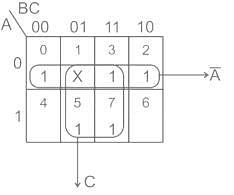




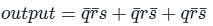
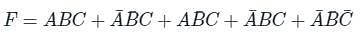
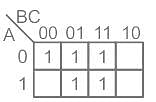
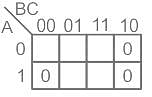

 can be minimized to
can be minimized to















