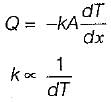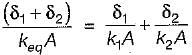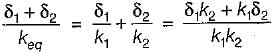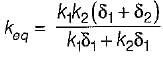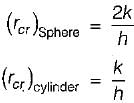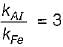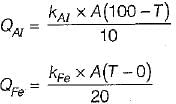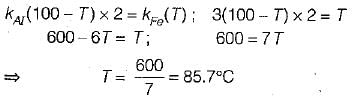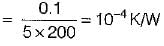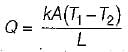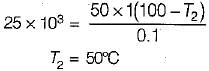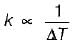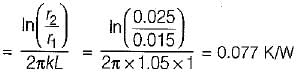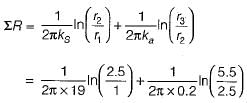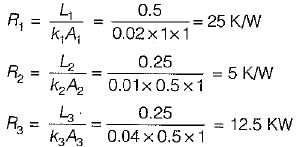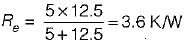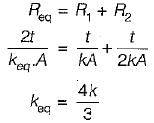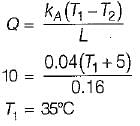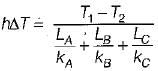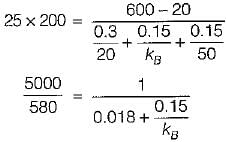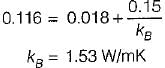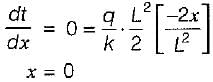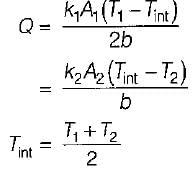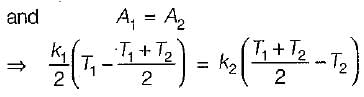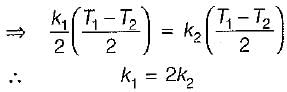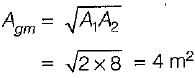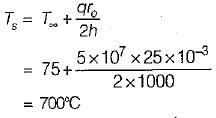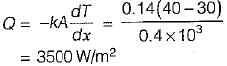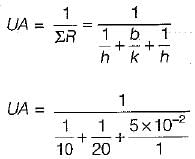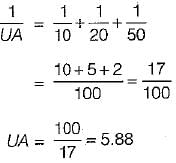Test: One-Dimensional Steady-State Conduction - 3 - Mechanical Engineering MCQ
30 Questions MCQ Test Topicwise Question Bank for Mechanical Engineering - Test: One-Dimensional Steady-State Conduction - 3
The critical thickness of insulation for sphere is given by
As the thickness of insulation around a heated cable gradually increases from zero, heat transfer from the conductor
Upto critical radius of insulation
A critical radius of insulated pipe leads to
If the radius of any current carrying wire is less than the critical radius, then the addition of electrical insulation will enable the wire to carry a higher current because
In case of hollow cylinder, as the ratio of outer radius to inner radius increases, the heat transfer
For a given heat flow and for the same thickness the temperature drop across the material will be maximum for
At steady state, the temperature variation in a plane wail, made of two different solids I and II is shown below figure.
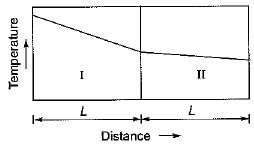
Then the thermal conductivity of material I
What is the equivalent thermal conductivity of a composite wall made of two layers of different material of thermal conductivity k1 and k2 and having thickness δ1 and δ2 respectively
An electronic device in the form of a wire is found to dissipate maximum heat when its outer most diameter = 32 mm. Keeping all the parameter same, it is proposed to use the same device in spherical form. The ideal diameter would be
An aluminium sheet of 10 mm thickness is brought into contact with an iron sheet of 20 mm thickness. The outer surface of aluminium is kept at 100°C. Where as the outer surface of iron is maintained at 0°C. if the ratio of thermal conductivity of aluminium and iron is 3 : 1, then the interface temperature in °C is
A metal wall has an area of 5 m2, thickness 10 cm and a thermal conductivity 200 W/mK, what is the value of thermal resistance of the wall in K/W?
A steel plate of thermal conductivity 50 W/m-K and thickness 10 cm passes a heat flux by conduction of 25 kW/m2. If the temperature of the hot surface of the plate is 100°C then what is the temperature of the cooler side of the plate?
A composite wall of a furnace has 3 layers of equal thickness having thermal conductivities the ratio of 1 : 2 : 4. What will be the temperature drop ratio across the three respective layer
A long Glass cylinder of inner diameter = 0.03 m and outer diameter = 0.05 m carries hot fluid inside. If the thermal conductivity of glass = 1.05 W/mK the thermal resistance (K/W) per unit length of the cylinder is
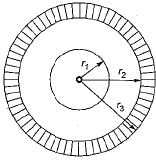
A stainless steel tube (ks = 19 W/mK) of 2 cm ID and 5 cm OD in insulated with 3 cm thick asbestos (ka = 0.2 W/mK). If the temperature difference between the inner most and outer most surface is 600°C the heat transfer rate per unit length is
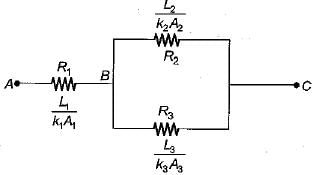
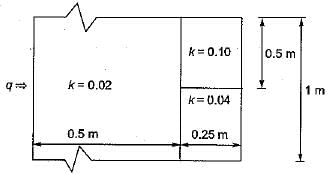
Heat flows through a composite slab, as shown below. The depth of the slab is 1 m. The k values are in W/mK. The overall thermal resistance in K/W is
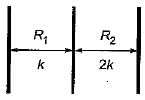
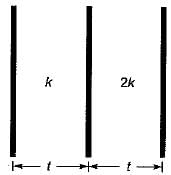
Two plates of equal thickness (t) and cross- sectional area, are joined together to form a composite as shown in the figure. If the thermal conductivities of the plates are k and 2k then, the effective thermal conductivity of the composite is
The heat flux (from outside to inside) across an insulating wail with thermal conductivity K = 0.04 W/mK and thickness 0.16 m is 10 W/m2. The temperature of the inside wall is -5°C. The outside wall temperature is
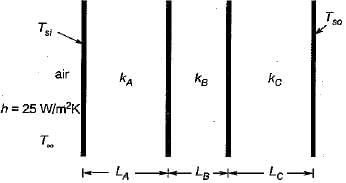
The composite wall of an oven consists of three materials A, B and C. Under steady state operating conditions, the outer surface temperature Tso is 20°C, the inner surface temperature Tsi is 600°C and the oven air temperature T∞ is 800 °C, For the following data: thermal conductivities kA = 20 W/(mK) and kC = 50 W/(mK), thickness LA = 0.3 m, LB = 0.15 m and LC = 0.15 m, inner-wall heat transfer coefficient h = 25 W/(m2K) the thermal conductivity kB (W/(mK) of the material B, is calculated as
For a plane wall of thickness l with uniformly distributed heat generation qg per unit volume, the temperature t0 at the mid-plahe is given by
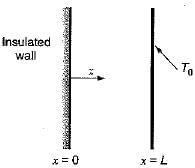
A slab of thickness L with one side (x = 0) insulated and other side (x = L) maintained at a constant temperature T0 is shown below:
A uniformly distributed internal heat source produces heat in the slab at the rate of W/m3. Assume the heat conduction to be steady state and 1 - D along the x-direction, the maximum temperature in the slab occurs at x equal to
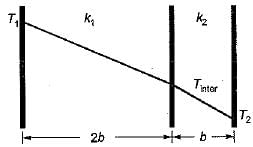
In a composite slab, the temperature at the interface (Tinter) between two materials is equal to the average of the temperature at the two ends. Assuming steady one dimensional heat conduction, which of the following statements is true about the respective thermal conductivities?
A metallic rod of uniform diameter and length L connects two heat sources each at 500°C. The atmospheric temperature is 30°C. The temperature gradient dT/dL at the centre of the bar will be
A hollow sphere has inner and outer surface areas of 2 m2 and 8 m2 respectively. For a given temperature difference across the surfaces, the heat flow is to be calculated considering the material of the sphere as a plane wall of the same thickness. What is the equivalent mean area normal to the direction of heat flow?
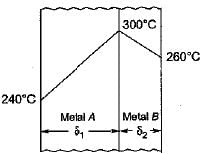
The temperature gradient through the two layer composite wall consisting of two metals A and B is as shown in figure. It can be concluded that
Heat is being transferred convectively flow through a cylindrical nuclear reactor fuel rod of 50 mm diameter to water at 75°C. Under steady state condition, the rate of heat generation within the fuel element is 5 x107W/m3 and the. convection heat transfer coefficient is 1 kW/m2 K. The outer surface temperature of the fuel element would be
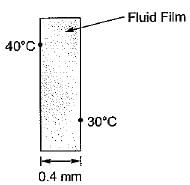
A stagnant liquid film of 0.4 mm thickness is held between two parallel plates. The top plate is maintained at 40°C and the bottom plate is maintained at 30°C. if the thermal conductivity of the liquid is 0.14 W/(m K), then the steady state heat flux (in W/m2) assuming one dimensional heat transfer is
A flat plate has thickness 5 cm, thermal conductivity 1 W/(mK) convective heat transfer coefficients on its two flat faces of 10 W/(m2K) and 20W/(m2K). The overall heat transfer coefficient for such a flat plate is
Steady state one dimensional heat flow by conduction as given by Fourier's low does not assume that
|
45 videos|314 tests
|



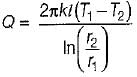
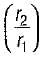 increases Q decreases
increases Q decreases