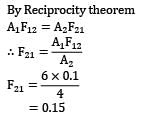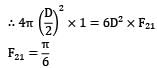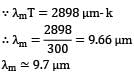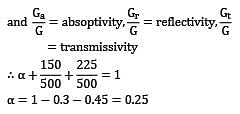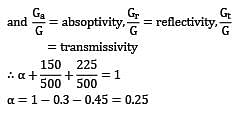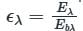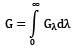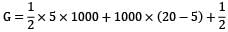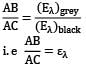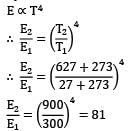Get the App Signup / Login
Sign in Open App

Test: Radiative Heat Transfer Level - 1


20 Questions MCQ Test Heat Transfer | Test: Radiative Heat Transfer Level - 1


Description
Attempt Test: Radiative Heat Transfer Level - 1 | 20 questions in 40 minutes | Mock test for Chemical Engineering preparation | Free important questions MCQ to study Heat Transfer for Chemical Engineering Exam | Download free PDF with solutions
QUESTION: 1

A radiator in a domestic heating system operates at a surface temperature of . Assuming the radiator behaves as a black body, the rate at which it emits the radiant heat per unit area is

(Assume σ =5.67 x 10-8 W/m2-k4)

 

Solution:

As per Stefan Boltzmann law

Eb = Q/A = σ x T4

Eb = 5.67 x 10-8 x (55 + 273)4

= 656.2 W/m2

≃ 0.66 kW/m2

QUESTION: 2

Sun’s surface at emits maximum spectral power for wavelength of A grey surface at a will Demit maximum spectral power at a wavelength of

Solution:

By Wien’s displacement law,

λm ∝ 1/T

∴ (λm)2/(λm)1 = T1/T2

∴ (λm)2 = (λm)1T1/T2

∴ (λm)2 = 0.5 x 5800/(300 + 273)

(λm)2 = 5.06μm

≃ 5μm

QUESTION: 3

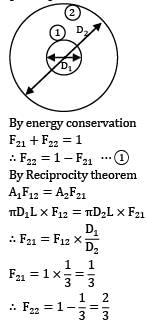
Two radiating surfaces A1= 6m2 and A2=4m2 have shape factor Then shape factor will be

Solution:

By Reciprocity theorem

A1F12 = A2F21

= 0.15

QUESTION: 4

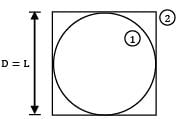
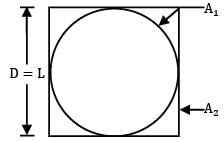
What will be the view factor for the geometry as shown in the figure (sphere within a hollow cube)?

 
Solution:

1 is a spherical surface

∴ F11 = 0

By summation rule,

F12 + F11 = 1

∴ F12 = 1

By Reciprocity theorem,

A1F12 = A2F21

QUESTION: 5

A radiation shield should
Solution:

A radiation shield should reflect back as much radiation as possible. Hence radiation shield should have high reflective power.

QUESTION: 6

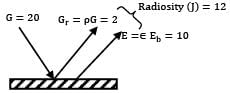
For an opaque plane surface at steady state the irradiation, radiosity and emissive power are respectively 20, 12 and . What is the emissivity of the surface?
Solution:

J = pG + εEb

For an opaque body

∵ α + ρ = 1

ρ = 1- α

∴ J = (1-α)G + εEb

By kirchoff’s law, α = ε

∴ J = (1-α)G + εEb

12 = (1- ε)20 + 10

ε = 0.9

QUESTION: 7

The wavelength for which the blackbody emissive power is maximum for a temperature of 300 K is
Solution:

By Wien’s displacement law,

∵ λmT = 2898 μm-k

λm ≃ 9.7μm

QUESTION: 8

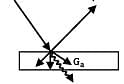
Solar radiation is incident on a semitransparent body at a rate of . If of this incident radiation is reflected back and is transmitted across the body, the absorptivity of the body is
Solution:

G = 500 W/m2 Gr = 150 W/m2

Gt = 225 W/m2

By energy conservation principle,

Ga+Ge+Gt = G

Where Ga = absorbed radiation

Gr = reflected radiation

Gt = transmitted radiation

G = incident radiation

= transmissivity

α = 1-0.3 - 0.45 = 0.25

QUESTION: 9

A grey body is defined such that
Solution:
QUESTION: 10

The minimum number of view factors that need to be known to solve a 10-surface enclosure completely, is
Solution:

For n-surface enclosure if nC2 view factors are known directly, entire enclosure can be solved. Thus for 10 surfaces, number of view factors that need to be evaluated directly will be

QUESTION: 11

The spectral distribution of surface irradiation is as follows

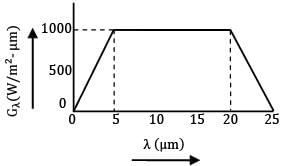
What is the total irradiation in kW/m2 ?
Solution:

Total irradiation is given as

i.e. it is equal to area under the curve Gλ Vs λ Hence,

x (25-20) x 1000

∴ G = 20000 W/m2

I.e. G = 20 kW/m2

QUESTION: 12

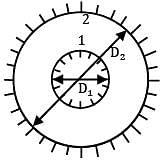
Consider two infinitely long blackbody concentric cylinders with a diameter ratio . The shape factor of the inner surface of outer cylinder with respect to itself will be
Solution:

By Energy conservation

F12 + F22 =1

∴ F22 = 1-F21 ….①

By Reciprocity theorem

A1F12 = A2F21

πD1L x F12 = πD2L x F21

QUESTION: 13

A large spherical enclosure has a small opening. The rate of emission of radiative flux through this opening is . The temperature at the inner surface of the sphere will be about (assume Stefan Boltzmann constant σ = 5.67 x 10-8 W/m2K4)
Solution:

A small opening in a large spherical enclosure behaves as a black surface

∴Eb = σT4

7350 = 5.67 x 10-8 x T4

T = 600K

I.e. T = 327oC

QUESTION: 14

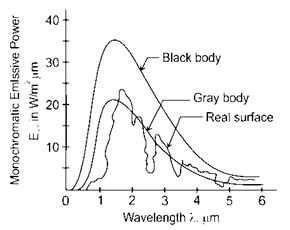
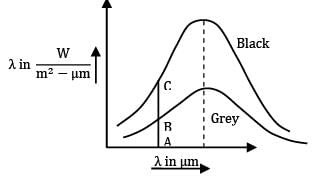
Consider monochromatic emissive power (Eλ) Vs Wavelength(λ) of a black and grey surface both at same temperature. The ratio AB/AC is given as
Solution:

AB & AC are monochromatic emissive power of grey and black surfaces for same wavelength. Hence, ratio is

which is monochromatic emissivity of grey surface.

QUESTION: 15

If the temperature of a solid surface changes from then its emissive power will increases in the ratio of
Solution:

By Stefan Boltzmann law

E ∝ T4

QUESTION: 16

Consider a hemispherical furnace. The view factor of it’s roof (hemisphere) with respect to itself is __________.
Solution:

By reciprocity theorem

A1F12 = A2F12

1 is a planar surface, i.e F11 = 0

∴ F12 = 1

Hence F21 = 0.5

F21 + F22 = 0.5

F22 + 1-0.5 = 0.5

QUESTION: 17

Fraction of radiative energy leaving one surface that strikes the other surface is called
Solution:
QUESTION: 18

Ice is very close to a
Solution:

The absorptivity of ice is 0.985, hence ice is very close to a black body

QUESTION: 19

For a grey diffuse surface with emissivity ε and temperature T, the intensity of emitted radiation is given as __________. ( is StefanBoltzmann constant.)

 
Solution:

For a diffuse surface, intensity of emitted radiation (Ie) is same in all directions and is given as

Ie = E/π

Where E is total emissive power

Therefore

Ie = εσT4/π

QUESTION: 20

Solar radiation of falls on a grey opaque surface at steady state. The surface has a temperature of and emissivity of 0.8. Find radiosity from the surface?

Solution:

J = E+Gr

E = εσT4

E = 0.8 x 5.67 x 10-8 x (50 + 273)4

E = 493.72 W/m2

Given G = 1200 W/m2

But as surface is at steady state

α = ε = 0.8

∴ ρ = 1 -α = 0.2

∴ Gr = ρG

Gr = 0.2 x 1200 = 240 W/m2

Therefore

J = E+Gr

J = 493.72 + 240

J = 733.72 W/m2

Use Code STAYHOME200 and get INR 200 additional OFF
Use Coupon Code
Use Coupon Code

Recommended Content

Download free EduRev App

Track your progress, build streaks, highlight & save important lessons and more!
© EduRev
Follow Us