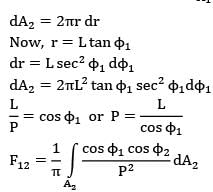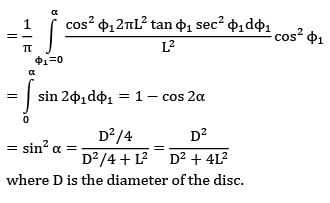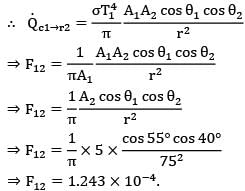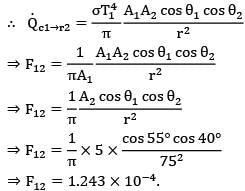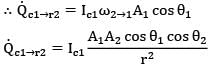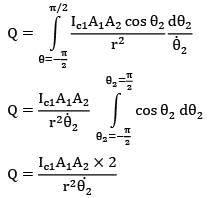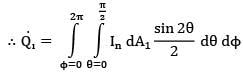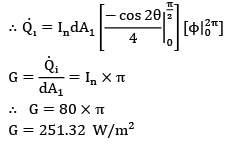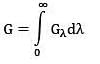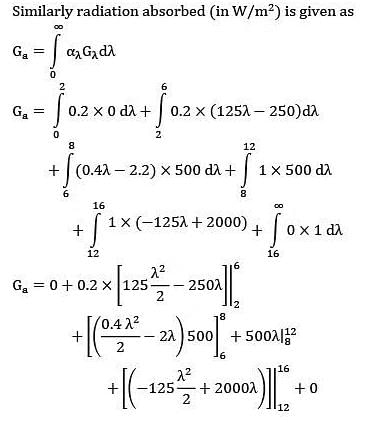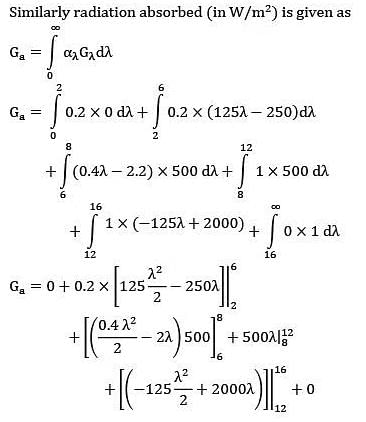Test: Radiative Heat Transfer Level - 3 - Mechanical Engineering MCQ
20 Questions MCQ Test Heat Transfer - Test: Radiative Heat Transfer Level - 3
The dark surface of a ceramic stove top may be approximated as a blackbody. The “burners,” which are integral with the stove top, heated from below by electric resistance heaters.
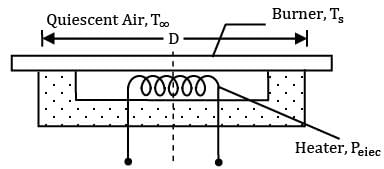
Consider a burner of diameter D = 200mm operating at a uniform surface temperature of Ts = 250oC in ambient air at . Without a pot or pan on the burner, if the efficiency associated with energy transfer from the heaters to the burners is , what is the electric power requirement? (The relation between Nusselt number and Rayleigh number is given as NuL = (RaL)¼)
Air (Tf = 408 K)
k = 0.0344 x W/mK
ν = 27.4 x 10-6 m2/s
α = 39.7 x 10-6 m2/s
Pr = 0.70
β = 0.00245 K-6

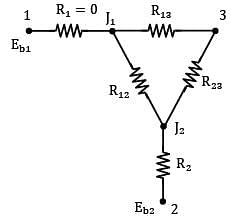
A metal storage tank with planar surfaces of external area contains water at and is located inside a large enclosure with walls at 65oC . The tank is initially painted black on the outside and its emissivity is approximated to 0.95. How much percentage reduction in heat loss would occur if the outside surface of tank is coated with aluminium paint (instead of black) of emissivity 0.55? Take radiation constant
σb = 5.67 x 10-8 W/m2K4
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
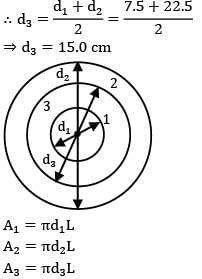
Two infinitely long cylinders are placed coaxially. The inner cylinder has an outside diameter of 7.5 cm, and emissivity of 0.1 and is maintained at 1050 K. The outer cylinder has an inside diameter of 22.5 cm, an emissivity of 0.2 and is maintained at 315 K. A cylindrical shield (very thin so that its temperature is the same on both sides) is placed concentrically midway between the two cylinders and allowed to come to thermal equilibrium. It has an emissivity of 0.3 on both sides. Assuming that vacuum exists between the annular spaces. Find the steady state temperature attained by the cylindrical shield.
The spectral emissivity of an opaque surface at 800 K is approximated as
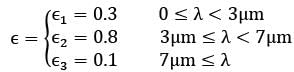
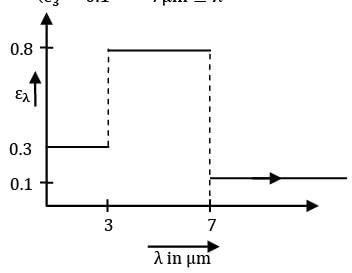
Black body radiation function values for a black surface at 800 K are as follows

Find the total emissivity of the surface?
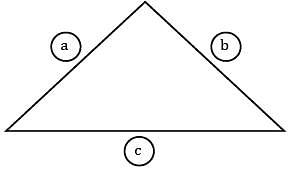
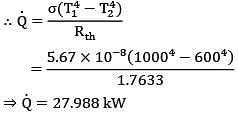
Consider an infinitely long three sided triangular enclosure with sides 2 cm, 3 cm and 4 cm. The view factor from 2 cm side to 4 cm side is __________.
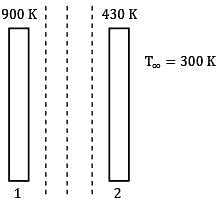
An industrial furnace employs a hollow brick lining. The inside and outside surfaces of the hollow brick lining are maintained at 900 K and 430 K by placing radiation shields in between the hollow space. The heat loss occurs to the surroundings (300 K) by both radiation and natural convection. Calculate number of shields needed. The emissivity of walls and shields can be taken as 0.85. The convective heat transfer coefficient is governed by the expression
h = 1.5(ΔT)0.33 W/m2- K
An electrically heated industrial furnace cavity is modeled in the form of a cylinder having diameter 10 cm and length 20 cm. It is opened at one end to the surrounding, that is at a temperature of 300 K. The electrically heated sides and the bottom of the cavity which are well insulated and may be approximated as black bodies, maintained at a temperature of 1800 K and 2000 K respectively. Find the power required to maintain the cylindrical surface at this condition. Take shape factor from the bottom surface to surroundings as 0.06.
A furnace is shaped like a long equilateral triangular duct. The width of each side is 1 m. The base surface has an emissivity of 0.7 and is maintained at a uniform temperature of 600 K . The heated left-side surface closely approximates a blackbody at . The right-side surface is well insulated. Determine the rate in kW at which heat must be supplied to the heated side externally per unit length of the duct in order to maintain these operating conditions.
Air is flowing inside a cylindrical tube in which a thermocouple is kept. Convective heat transfer coefficient between air and thermocouple is 60 W/m2- C, εthermocouple = 0.5, εwall = 0.6. If Ta = 970o C and Tc = 800oC then, Tw is ________. Air is a non-participating medium in terms of radiation
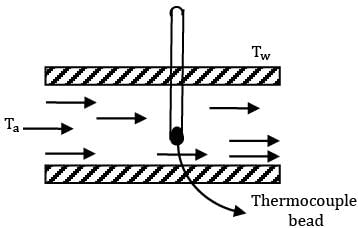 (Tc)
(Tc)
Option~
(A) 1041.7oC
(B) 1000oC
(C) 768.7oC
(D) 509oC
If is the emissivity of surfaces and shields and n is the number of shields introduced between the two surfaces, then overall emissivity is given by
Option~
(A) n/ε
(B) 1/(2n-ε)
(C) nε
(D) ε/[(n+1)(2-ε)]
The net radiation from the surfaces of two parallel plates maintained at is to be reduced by at least 99%. Number of shields which should be placed between surfaces to achieve this reduction is (εshield = 0.05), (εsurface = 0.8)
Option~
(A) 3
(B) 4
(C) 5
(D) 6
In the previous question if εshield = εsurface, then what will be the number of shields?
Option~
(A) 100
(B) 3
(C) 99
(D) 4
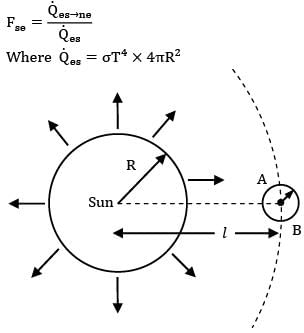
Consider sun (radius R) to be a black body of temperature T. Find out the view factor of earth ( with respect to sun. The center to center distance between sun and earth is (l >>r,R).
Option~
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
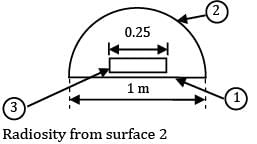
A cake is being baked in an hemispherical oven of radius 500 mm. The lower surface of the oven is maintained at 1000 K while the covering surface ( is maintained at 800 K. The diameter of the round cake is 0.25 m and its height can be neglected. Considering the lower surface of the oven and cake to be black bodies and neglecting the area covered by the cake, find the time required to bake the cake, if it requires 3.2123 MJ.
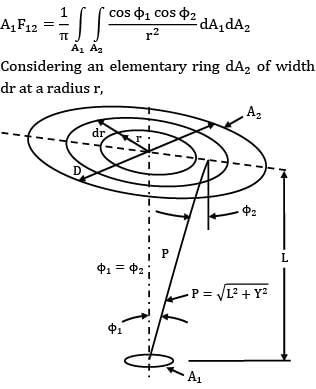
Determine the shape factor between a small area and a parallel circular disc A2(diameter D) is located on the axis of the disc and the semi-vertex angle of the cone formed with the disc as base and as the vertex is α.
Option~
(A) 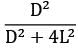
(B) ![]()
(C) 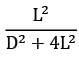
(D) ![]()
A small surface of area emits radiation as a blackbody at temperature T1 = 600 K. A fraction of energy emitted by A1 strikes another small surface of area A2 = 5 cm2 oriented as shown in the figure
A1 = 3 cm2
T1 = 600 K
Find out view factor of surface with respect to A1 ?
Option~
(A) 0.6215 x 10-4
(B) 1.234 x 10-4
(C) 4.14 x 10-4
(D) 2.071 x 10-4
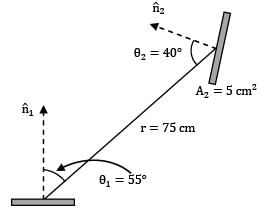
A small surface of area emits radiation as a blackbody. A fraction of this energy emitted is received by another small area Oriented as shown in figure.
A1 = 2 cm2
The rate at which radiation emitted by surface 1 strikes is measured to be 274 x 10-6 W. Determine the surface temperature of in K?
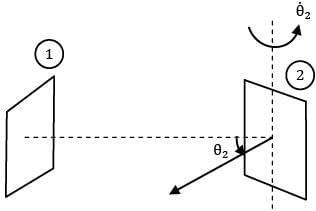
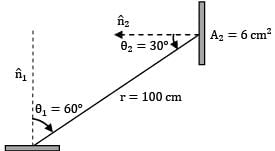
A small stationary surface of area A1 = 10-4m2 emits diffusely with a total intensity of . A second surface of equivalent area is located at a fixed distance from . The connecting line between the two surfaces remains perpendicular to while rotates at an angular frequency of
ፀ2 = dፀ2/dt = 2 rad/s about the axis as shown in the figure.
What is the amount of energy intercepted by the two sides of , during one complete revolution?
Option~
(A) 2 x 10-6j
(B) 4 x 10-6j
(C) 8.0 x 10-6j
(D) 16 x 10-6j
On an overcast day the directional distribution of the solar radiation incident on the earth’s surface may be approximated by an expression of the form where In = 80 W/m2is the total intensity of radiation directed normal to the surface and is the zenith angle. What is the solar irradiation at the earth’s surface?
The spectral, hemispherical absorptivity of an opaque surface and the spectral irradiation at the surface are as shown.
 λ(μm)
λ(μm) λ(μm)
λ(μm)
What is the total hemispherical absorptivity of the surface?
|
57 videos|77 docs|86 tests
|
|
57 videos|77 docs|86 tests
|


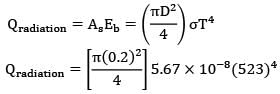

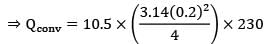

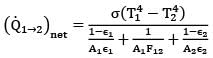
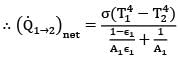
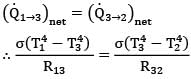
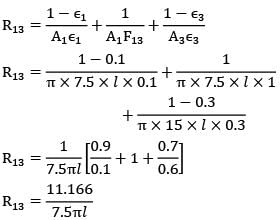
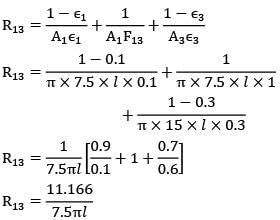
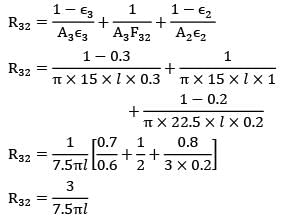
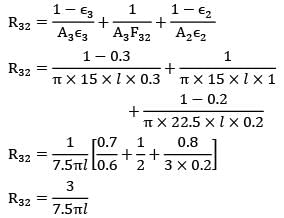
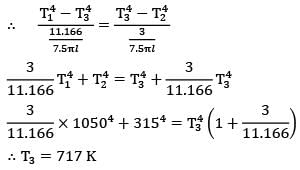
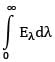

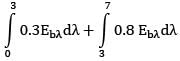
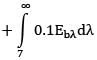
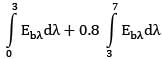
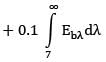

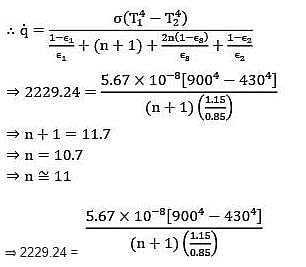

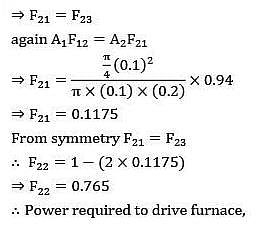

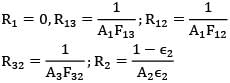
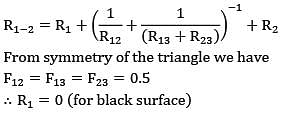
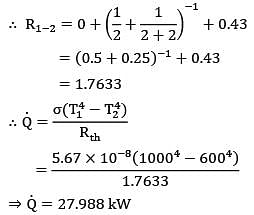
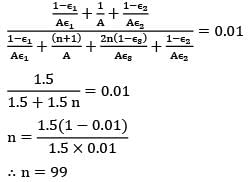
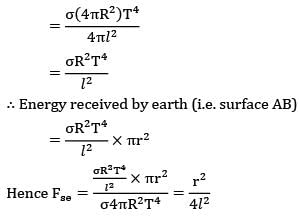
 ’
’