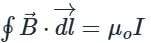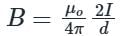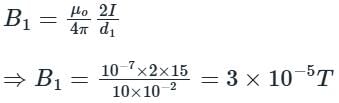Test: Ampere Law & Maxwell Law - Electrical Engineering (EE) MCQ
20 Questions MCQ Test - Test: Ampere Law & Maxwell Law
Electric field will be maximum outside the conductor and magnetic field will be maximum inside the conductor. State True/False.
Find the magnetic flux density of a finite length conductor of radius 12cm and current 3A in air( in 10-6 order)
Calculate the magnetic field intensity due to a toroid of turns 50, current 2A and radius 159mm.
Find the magnetic field intensity due to an infinite sheet of current 5A and charge density of 12j units in the positive y direction and the z component is below the sheet.
Find the current density on the conductor surface when a magnetic field H = 3cos x i + zcos x j A/m, for z>0 and zero, otherwise is applied to a perfectly conducting surface in xy plane.
When the rotational path of the magnetic field intensity is zero, then the current in the path will be
Find the magnetic field intensity when the current density is 0.5 units for an area up to 20 units.
Find the charge density when the electric flux density is given by 2x i + 3y j + 4z k.
Find the Maxwell equation derived from Faraday’s law.
In which of the following forms can Maxwell’s equation not be represented?
The charge build up in the capacitor is due to which quantity?
In metals which of the following equation will hold good?
Find the flux enclosed by a material of flux density 12 units in an area of 80cm.
Find the electric flux density of a material with charge density 16 units in unit volume.
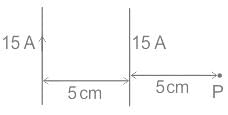
If the distance between the two long straight wires is 5 cm, with each carrying a current of 15 A in the same direction, then find a magnetic field at P