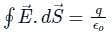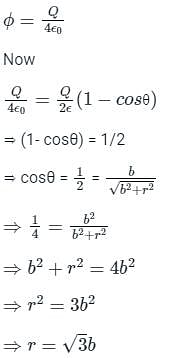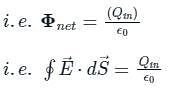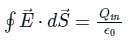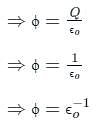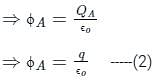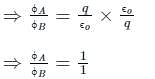Test: Gauss's Law - Electrical Engineering (EE) MCQ
10 Questions MCQ Test Electromagnetic Fields Theory (EMFT) - Test: Gauss's Law
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
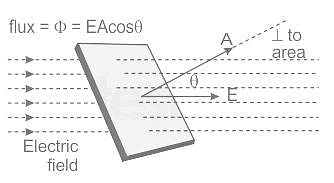
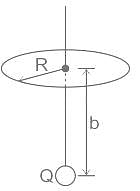
A point charge Q is located on the axis of a disk of radius R at a distance b from the plane of the disk as shown in below figure. Find the value of R, if 1/4th of the electric flux from the charge passes through the disk?

The electric flux from a cube of side ‘a’ is ‘Φ’. What will be its value if the side of the cube is made ‘2a’ and the charge enclosed is made half?
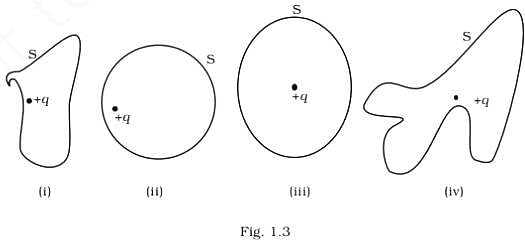
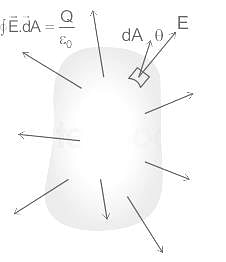
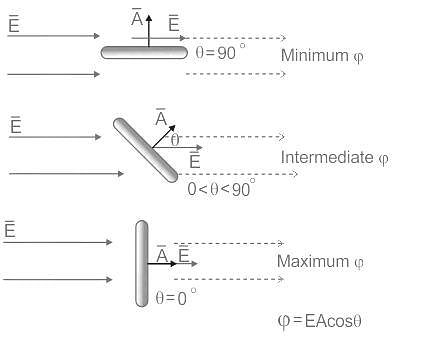
According to gauss theorem, the electric flux on a closed surface depends on?
The net electric flux through a spherical surface having 10 μC charge at the centre is
If a unit positive charge is placed inside a sphere of radius r, then the electric flux through the sphere will be:
The total electric flux through a closed surface in which a certain amount of charge is placed depends on the:
The charge enclosed in the two cubes A and B is q. If ratio of the surface area of cubes A to cube B is 1 : 2, then the ratio of the flux associated with cube A to cube B will be:
|
10 videos|45 docs|56 tests
|
|
10 videos|45 docs|56 tests
|