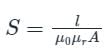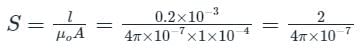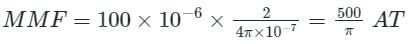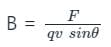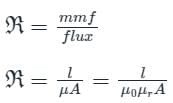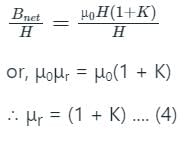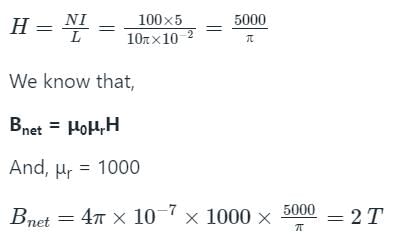Test: Magnetomotive Force - Electrical Engineering (EE) MCQ
10 Questions MCQ Test - Test: Magnetomotive Force
A magnetising force of 800 AT/m will produce a flux density of ______ in air.
In order to produce a flux of 100 μwb in an air gap of length 0.2 mm and area of cross-section is 1 cm2, the MMF required is:
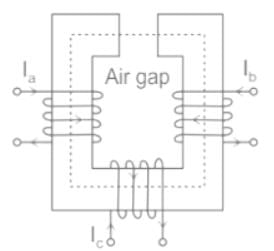
A rectangular iron core has three coils as shown in the given figure. The number of turns of the coils are Na = 300, Nb = 600 and Nc = 600, and the respective currents are 1.5 A, 4 A and 3 A. Find the total magnetomotive force.
Considering electromagnetic circuits, which of the following is unit less?
If an electron, a neutron and a proton having same momenta enter perpendicularly to a magnetic field, then:
The property of a material which opposes the production of magnetic flux is called
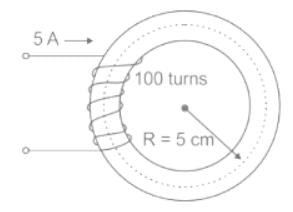
In the magnetic circuit shown below, what is the flux density produced if the relative permeability of the core material under the given condition is 1000?
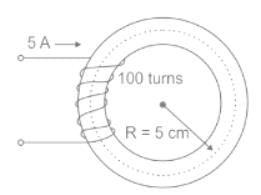
If the two conductors carry current in opposite directions, there will be