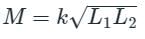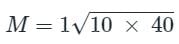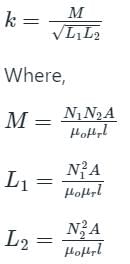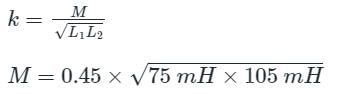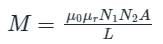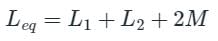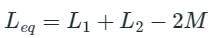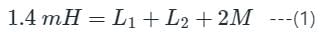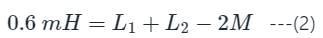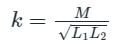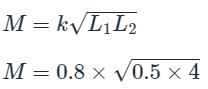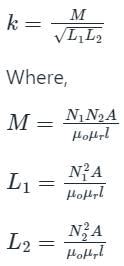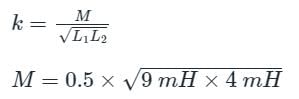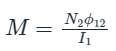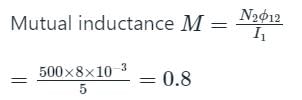Test: Mutual Inductance - Electrical Engineering (EE) MCQ
10 Questions MCQ Test - Test: Mutual Inductance
Two coils having self-inductances of 10 mH and 40 mH are mutually coupled. What is the maximum possible mutual inductance?
Two inductors L1 = 20 mH and L2 = 40 mH are connected in series so that their equivalent inductance is 50 mH. The mutual inductance between the two coils is _______.
The coefficient of coupling between two coils is 0.45. The first coil has an inductance of 75 mH and the second coil has an inductance of 105 mH. What is the mutual inductance between the coils?
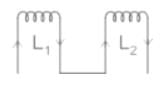
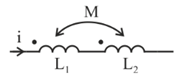
The effective inductance of two coils with self inductances L1, L2 and mutual inductance M (as connected shown in figure) will be:

Identify the INCORRECT statement among the given options regarding mutual inductance.
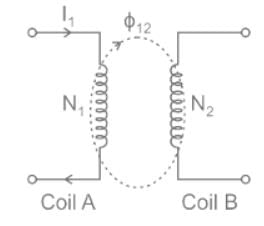
Which of the following devices does not work on the principle of mutual induction?
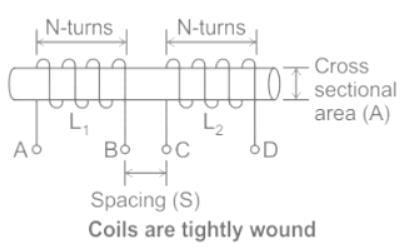
The total inductance of two coupled coils in the ‘series aiding’ and ‘series opposing’ connections are 1.4 × 10-3 Henry and 0.6 × 10-3 Henry, respectively. The value of mutual inductance will be:
Two coupled coils with L1 = 0.5 H and L2 = 4.0 H have a co-efficient of coupling 0.8. Find maximum value of the inductance EMF in the coil 2 if a current of i1 = 20 sin 314t A is passed in coil 1.
The self inductance of two coils are 4mH and 9mH respectively. If the coefficient of coupling is 0.5, the mutual inductance between the coils is _____
Two identical coils X and Y of 500 turns each lie in parallel planes such that 80% of flux produced by one coil links with the other. If a current of 5 A flowing in X produces a flux of 10 mWb in it, find the mutual inductance between X and Y