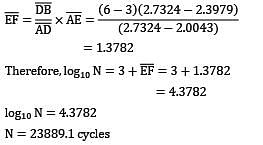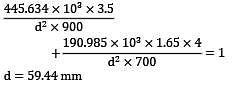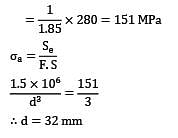Test: Design For Static And Dynamic Load Level - 3 - Mechanical Engineering MCQ
20 Questions MCQ Test Design of Machine Elements - Test: Design For Static And Dynamic Load Level - 3
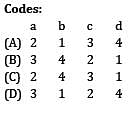
Match List-I (Mechanical Property) with List-II (Measured in Terms of) and select the correct answer using the codes given below the lists.


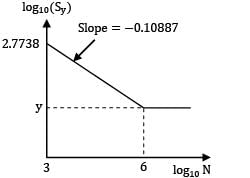
A S-N curve for steel is shown in figure. The corrected endurance limit is
Sy: Yield strength in MPa.

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A forged steel bar of 50 mm diameter, is subjected to a reversed bending stress of 250N/mm2 . The bar is made of steel 40 C8 mm (Sut = 600 N/mm2)and the corrected endurance limit of the bar is 101N/mm2 , then life of the steel bar will be __________ cycles.
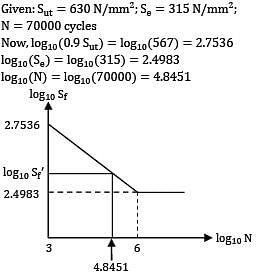
A rotating bar of steel (Sut = 600N/mm2) is subjected to a completely reversed bending stress. The corrected endurance limit of the bar is 315N/mm2 . The fatigue strength (in N/mm2) of the bar for a life of 70000 cycles is __________
When st!ess and Young’s Modulus of Elasticity E remain constant, the energyabsorbing capacity of part subjected to dynamic axial forces, is a function of its
Fatigue strength of a rod subjected to cyclic axial force is less than that of a rotating beam of the same dimensions subjected to steady lateral force. What is the reason?
A flat plate is subjected to a tensile force of 10kN. The permissible stress in the plate is 100N/mm2
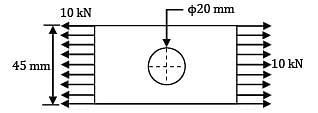
The stress concentration factor of hole section is 2.1. The thickness of plate is __________ mm.
A component is subjected to a dynamic stress given by 200 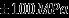 a. The material is ductile and has the following properties
a. The material is ductile and has the following properties
Sut = 600MPa, Syt = 400MPa, Se = 300MPa
The factor of safety based on Goodman’s and Soderberg’s criteria are respectively
A ductile material having an endurance limit of 200N/mm2 and the yield limit is 300N/mm2 , is stressed under variable load. The maximum and minimum stressed are 150N/mm2 and 50N/mm2 . The fatigue stress concentration factor is 1.3. The factor of safety for this loading is __________.
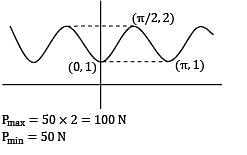
A plate made of grey cast iron in hot-rolled and normalized condition. It is subjected to a axial load of (1+sin2x) . The amplitude ratio will be __________ (upto two decimal places).
A component is subjected to a flexural stress which fluctuates between 310N/mm2 and -160N/mm2 . If endurance strength is half of the ultimate strength, the minimum ultimate strength according to Gerber relation is (Factor of safety = 2)
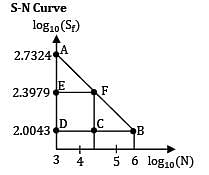
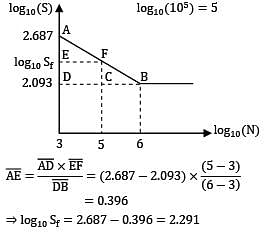
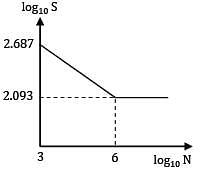
A cantilever beam is subjected to completely reversed bending moment of 200 Nm. The log S log N diagram for the beam is shown in the figure. The diameter d of the beam for a life of 105 cycles is
A steel connecting rod is subjected to a completely reverse axial load of 100 kN. For the steel material Su = 1100MP a, Sy = 930MPa,Se = 0.5, Su.load factor 0.85, Size factor 0.85 and su!face finish factor = 0.76. What is the suitable size of the rod using a factor of safety 2?
(A) 30 mm
(B) 45 mm
(C) 60 mm
(D) 75 mm
A shaft of diameter d is subjected to a torque varying between 100 N.m to 500 N.m. Stress concentration factor due to keyway is 1.5.
Taking factor of safety 2 yield strength 300 MPa and endurance limit of 200 MPa. Correction factor for torsion is . , Surface finish factor for torsion is 0.6 and Surface finish factor is 0.85, and size factor is 0.82 The diameter of the shaft (mm) will be __________
A uniform bar having a machined surface is subjected to an axial load varying from 400 kN to 150 kN. The material of the bar has Su= 630 MPa,kc = 0.7 and kf= 1.42 Using Goodman’s Criteria and factor of safety 1.5, The diameter of the rod is __________ mm, Where, Su = ultimate tensile strength,kc = surface finish factor, kf = fatigue st!ess concentration factor
A bar of circular cross-section is subjected to alternating tensile forces varying from a minimum of 200 kN to a maximum of 500 kN. It is to be manufactured of a material with an ultimate tensile strength of 900 MPa and an endurance limit of 700 MPa. Using safety factors of 3.5 related to ultimate tensile strength and 4 related to endurance limit and a stress concentration factor of 1.65 for fatigue load. Using Goodman straight line as basis for design, the diameter of circular bar is
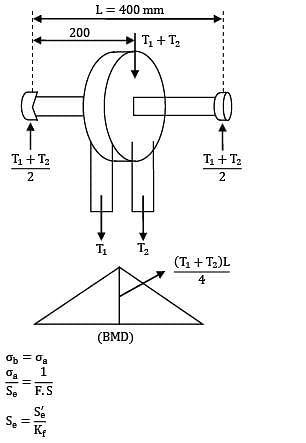
A pulley is supported midway between the two bearings spaced 400 mm apart on a shaft rotating at 1400 rpm. The tensions acting vertically downwards on the tight and slack side of the belt are 1000 N and 500 N respectively. The material of the shaft is 30 C8 steel with Se= 280MPa,Su = 600MPa,
kf = 1.85 FOS = 3, the diameter of the shaft
Bending stress in a machine component fluctuates between a tensile stress of 280 MPa and compressive stress for 140 MPa. The factor of safety is 1.75. The yield strength is equal to 55% of ultimate tensile strength and endurance strength is 50% of ultimate tensile strength. What should be the minimum ultimate tensile strength to carry this fluctuation indefinitely according to Soderberg’s criterion?
(A) 1155 MPa
(B) 955 MPa
(C) 725 MPa
(D) 575 MPa
A steel plate is subjected to a completely reversed axial load of 40 kN and it has 10 mm diameter hole. Width of the plate is 60 mm. If surface finish factor (ka) = 0.65 size factor (kb) = 0.75 Reliability factor (kc) = 0.789, Notch sensitivity (q) =.0.82 and theoretical stress concentration factor (kt) = 2.5. The ultimate tensile strength of the material (Sut) is 400 MPa. If the factor of safety is 2. What will be the thickness of the plate for infinite life (Take endurance limit as 50% of ultimate tensile strength and correction factor for axial load is 0.82)
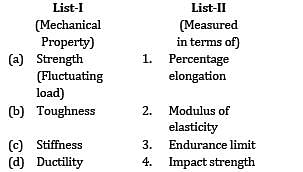
A circular bar of 500 mm length is supported by a hinge at its two ends. It is acted upon by a central cyclic load having a minimum value of 20 kN and a maximum value of 50 kN. The material properties of bar are given by: Ultimate strength of 650 MPa, yield strength of 500 MPa and endurance strength of 350 MPa. Taking a factor of safety of 1.5, size effect of 0.85, surface finish factor of 0.9, the diameter of the bar as per Goodman’s criteria is __________ mm
(A) 59
(B) 60.50
|
49 videos|70 docs|77 tests
|
|
49 videos|70 docs|77 tests
|