Test: Dot Product And Cross Product - Civil Engineering (CE) MCQ
30 Questions MCQ Test Engineering Mechanics - Test: Dot Product And Cross Product
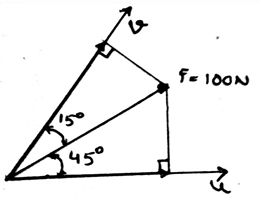
Determine the magnitude of the projection of the vector force F = 100N, onto the u axis, from the figure given below.
For two vectors A and B, what is A.B (if they have angle α between them)?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Which is true for two vector A = A1i + A2j + A3k and B = B1i + B2j + B3k?
Determine the magnitude of the force F = 300j parallel to the direction of AB?
What is {(i.i) + (-i.j) + (-k.k) + (k.i)}.(Ai +Bj + Cz)?
What is the value of {(AxB).(C.D)x(AxB).(C.D)}? For the four vectors A, B, C and D, with A, B, C and D all lying in the same plane?
What is (AxB).(BxA); or A = A1i + A2j + A3k and B = B1i + B2j + B3k?
What is the value of θ in the figure given below ?
Refer to the diagram given below, determine the magnitude of the force F = 300j perpendicular to the direction of AB.
Determine the magnitude of the projection of the vector force F = 100N, onto the v axis, from the figure given below.
What is the dot product of two vectors which are having magnitude equal to unity and are making an angle of 45°?
Mathematically, for two vectors A and B of any magnitude, the cross product of both, i.e. AxB = given by:
Commutative law is valid for the cross product of two vectors. (Commutative law: PxQ = QxP; for two vectors P and Q)
Which among the following is the distributive law for the cross product of three vectors?
Which statement is true? (For three vectors P, Q and R)
The ___________ forces do not cause the rotation.
The tendency of a force to rotate the body is called the moment of the force.
The moment is the cross product of which two vectors?
What is Varigon’s Theorem? (M = Moment, F= Force vector, R= Radius vector)
What is the mixed triple product of three vectors?
What is the angle made by the vector shown in the figure, with the z-axis?
What is the dot product of the components of the force vector shown in the figure, i.e. the dot product of the z-axis component and the y-axis component of the force?
What is the magnitude of the resultant vector’s unit vector? (Resultant vector of the two vectors shown in the figure below)
|
24 videos|59 docs|53 tests
|
|
24 videos|59 docs|53 tests
|

















