Test: Moment Of A Force - 2 - Civil Engineering (CE) MCQ
20 Questions MCQ Test Engineering Mechanics - Test: Moment Of A Force - 2
Which of the following is correct in the determination of the moment direction by curling of wrist?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
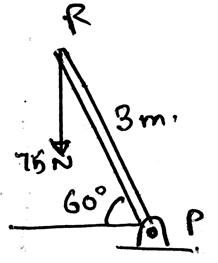
For the below diagram determine the magnitude of the horizontal force applied at R which creates the same moment at P as by 75N.
The moment axis is in the direction parallel to the plane of the force and the distance.
Determine the resultant moment caused by the forces in vector
Which of the following is correct w.r.t the moment (M) of the force (F) acting on the body at a distance L from the axis of the rotation?
What does FLsinθ means/represents for the moment (M) of the force (F) acting on the body at a distance L from the axis of the rotation?
The basic way of getting the direction of the moment caused by the force is:
If any force is applied in the direction of the positive x-axis, and there are three different point on which the moment of this force is to be calculated. Then if these three points are on the positive side of the y-axis with varying distance, then what will be the direction of the moment caused by the force to the individual point?
If a force applied at any point in its line of action and is still creating the same moment about any fixed point say P, then the force is said to be______________
If a force applied at any point in its line of action and is still creating the same moment about any fixed point say P, then the force is said to be sliding vector. What is the name of this property?
If a 12m high tree is being pulled by the tractor, by a rope tied over the top. With the tractor at a linear distance of 12m and 4m away perpendicularly from the tree. If the force applied by the tractor is 2KN then what is the moment caused about the roots of the tree?
If F = F1+F2, then moment of this force F about a point at a distance r is M=rxF1 + rxF2.
Determine the moment about the point Q by the force shown as 400N.
Determine the magnitude of the resultant moment caused by the forces.
|
24 videos|59 docs|53 tests
|
|
24 videos|59 docs|53 tests
|

















