Test; Moment Of A Force On A Specified Axis - Civil Engineering (CE) MCQ
15 Questions MCQ Test Engineering Mechanics - Test; Moment Of A Force On A Specified Axis
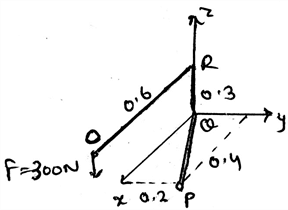
Determine the moment’s magnitude produce by the force as shown in the diagram, which tends to rotate the rod ORQP along QP.
The calculation of the moment about the axis and the moment about any point by a force applied on the body are different from each other.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In the calculation of the moment of the force about the axis, the cross product table, i.e. the 3X3 matrix which is made for doing the cross product having 3 rows, contains three elements. Which are they from top to bottom?
Which of the following is correct? (For A representing the vector representation of the axis of rotation, r the radius vector and F the force vector)
In the equation A.(rxF), the r vector is what?
The axis vector in the calculation of the moment along the axis of rotation is the axis which is collinear with the force vector.
What if the perpendicular distance from the axis is infinity?
In the equation A.(rxF) the r is heading from ______________ and ending at _____________
What if the moment of the force calculated about the axis is negative?
Determine the moment MQP in the vector form produce by the force as shown in the diagram, which tends to rotate the rod ORQP along QP.
Determine the moment of the force F along the segment QP of the pipe assembly shown in the figure.
Determine the magnitude of the moment of the force about the axis PQ.
Determine the magnitude of the moment of the force about the y-axis.
The ___________ forces do not cause the rotation if the rotation is considered in about the axis of the body or the centroid axis of the body.
|
24 videos|59 docs|53 tests
|
|
24 videos|59 docs|53 tests
|

















