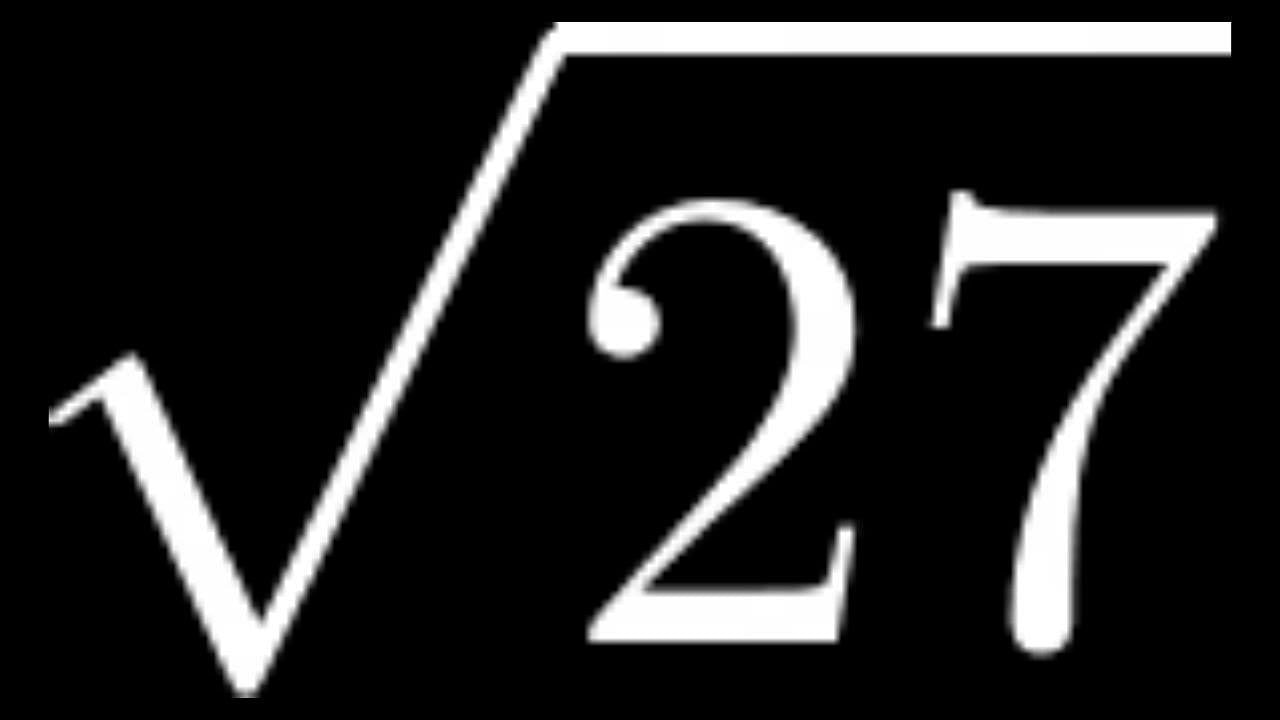|
Card: 2 / 40 |
The square root of 36 is 6, because 6 multiplied by itself (6 * 6) equals 36. Therefore, √36 = 6.  |
|
Card: 4 / 40 |
You can multiply square roots by multiplying the values inside the square roots. For example, √a * √b = √(a*b). |
|
Card: 7 / 40 |
Solve for z: √(z + 5) = 7. Hint: Square both sides to eliminate the square root. |
|
Card: 8 / 40 |
Squaring both sides gives (√(z + 5))² = 7², which simplifies to z + 5 = 49. Subtracting 5 from both sides gives z = 44. |
|
Card: 10 / 40 |
The square root of 49 is 7, because 7 multiplied by itself (7 * 7) equals 49. Therefore, √49 = 7.  |
|
Card: 12 / 40 |
(a + b)² = a² + 2ab + b². This is useful for expanding expressions that include square roots. |
|
Card: 17 / 40 |
If y = 25, what is √(y - 20)? Hint: Substitute y into the expression and simplify. |
|
Card: 20 / 40 |
The square root of 0 is 0, because 0 multiplied by itself equals 0. Therefore, √0 = 0. |
|
Card: 22 / 40 |
You can only subtract square roots if the values inside the square roots are the same. For example, √a - √a = 0, but √2 - √3 cannot be simplified further. 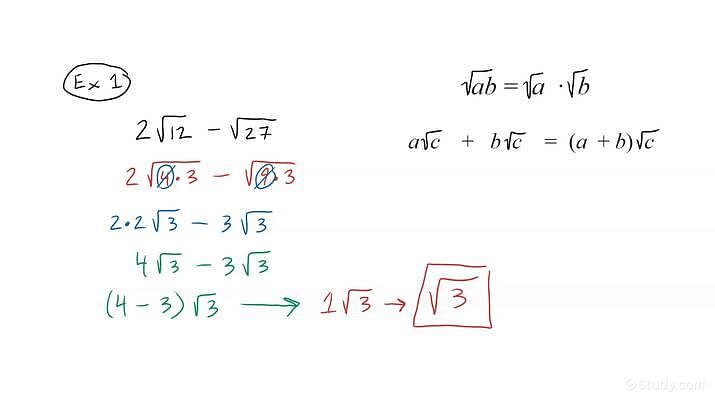 |
|
Card: 23 / 40 |
If x = 4, what is √(x² + 4)? Hint: Substitute x into the expression and simplify. |
|
Card: 26 / 40 |
The square root of 144 is 12, since 12 multiplied by itself (12 * 12) equals 144. Therefore, √144 = 12. 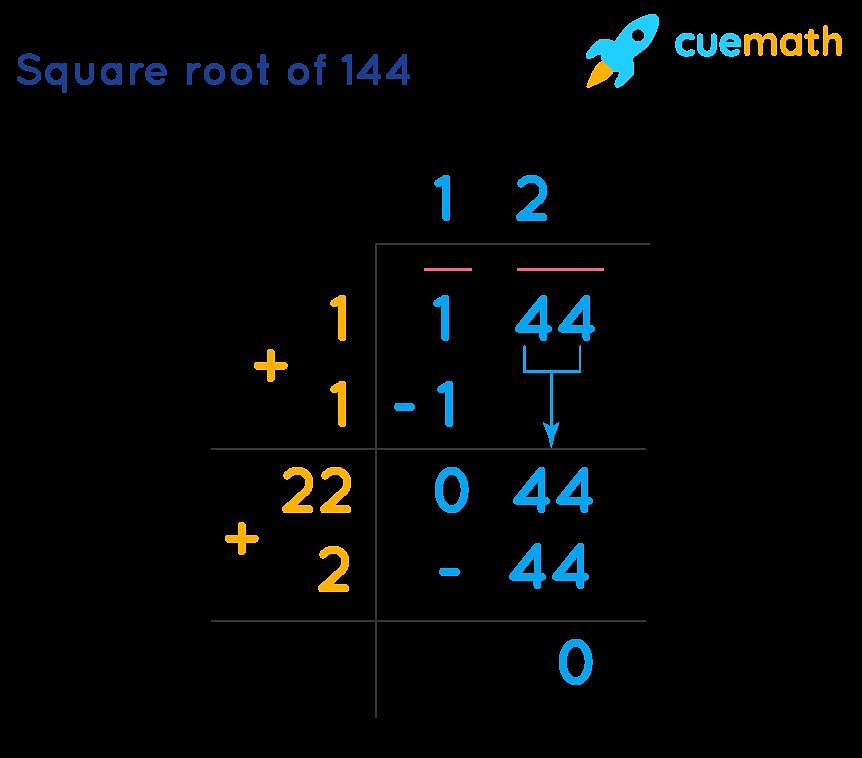 |
|
Card: 27 / 40 |
If z = 81, what is √(z/9)? Hint: Substitute z into the expression and simplify. |
|
Card: 33 / 40 |
If a = 16, what is √(a + 15)? Hint: Substitute a into the expression and simplify. |
|
Card: 36 / 40 |
The square root of 1 is 1, because 1 multiplied by itself equals 1. Therefore, √1 = 1. |
|
Card: 37 / 40 |
If b = 36, what is the value of √(b) - √(16)? Hint: Calculate each square root separately. |
|
Card: 40 / 40 |
The square of the square root of x is x itself, given that x is non-negative. Therefore, (√x)² = x. |