|
Card: 4 / 48 |
Square numbers are obtained by multiplying a number by itself, and they can be represented visually as dots arranged in a square shape. |
|
Card: 5 / 48 |
Fill in the blank: The first triangular number is ___ and is equal to the sum of the first ___ natural number. |
|
Card: 7 / 48 |
True or False: The sum of the first three odd numbers is equal to the third square number. |
|
Card: 9 / 48 |
What relationship exists between consecutive triangular numbers and square numbers? |
|
Card: 11 / 48 |
Riddle: I am a number that can be arranged in a triangle, and I represent the sum of the first n natural numbers. What am I? |
|
Card: 17 / 48 |
Fill in the blank: The second square number is ___ and can be represented as the sum of the first ___ odd numbers. |
|
Card: 24 / 48 |
They enhance the original beauty by repeating a certain shape or unit in one direction.  |
|
Card: 29 / 48 |
Riddle: I am formed by repeating shapes, enhancing beauty in every place. What am I? |
|
Card: 31 / 48 |
Fill in the blank: Square numbers are seen on a diagonal line in a ___ square. |
|
Card: 34 / 48 |
They create aesthetic appeal and can convey cultural significance through their repeated motifs. |
|
Card: 36 / 48 |
Square numbers are derived from the sum of two consecutive triangular numbers. |
|
Card: 37 / 48 |
Fill in the blank: Symmetry in patterns can be categorized into ___ and ___ reflections. |
|
Card: 40 / 48 |
False. Border patterns can be observed in various forms, including floors and wallpapers.  |
|
Card: 42 / 48 |
A tiling pattern is formed by the repetition of a single unit or shape that fills a plane completely without gaps or overlaps. 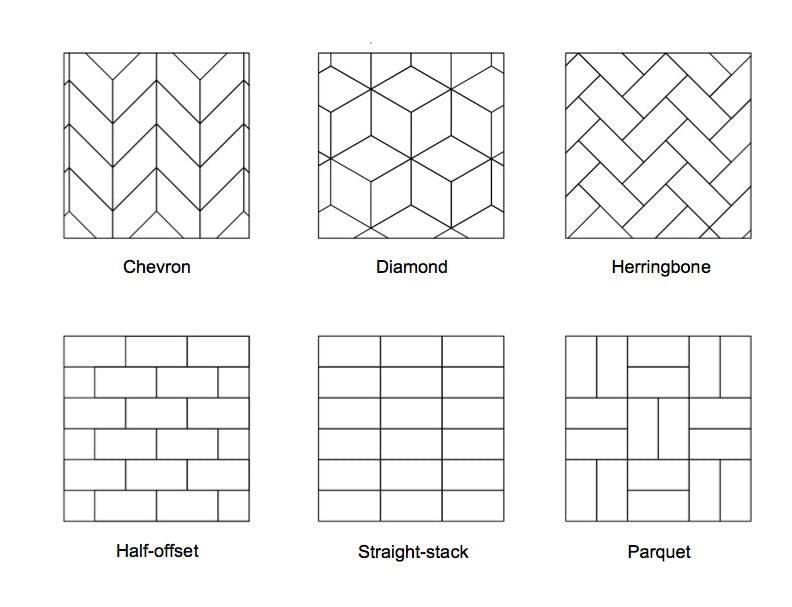 |
|
Card: 43 / 48 |
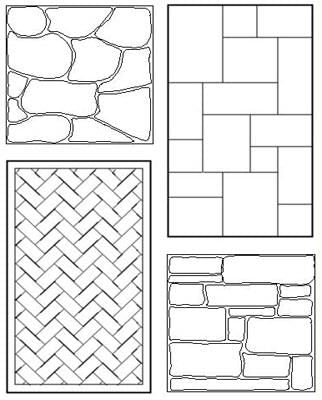
Fill in the blank: Patterns formed by pairing stones or bricks are familiar examples of ___. |
|
Card: 46 / 48 |
False; only those patterns that fill a plane without gaps and overlaps are considered tiling patterns.  |
|
Card: 48 / 48 |
A tiling pattern does not have any gaps or overlaps in the arrangement of its repeating units, whereas a non-tiling pattern does.  |