|
Card: 2 / 50 |
Common multiples are numbers that are multiples of two or more numbers. For example, the common multiples of 3 and 5 are 15, 30, 45, etc., because these numbers can be divided by both 3 and 5 without leaving any remainder. |
|
Card: 3 / 50 |
Common factors of two numbers are defined as numbers that ___ both numbers exactly without leaving a remainder. |
|
Card: 5 / 50 |
In the Idli-Vada game, what should a player say when they reach a number that is a multiple of both 3 and 5? |
|
Card: 7 / 50 |
True or False: The game 'Idli-Vada' continues until all players successfully say the correct numbers without mistakes. |
|
Card: 9 / 50 |
In the context of the Idli-Vada game, what does a player say when they reach a number that is a multiple of 3? |
|
Card: 11 / 50 |
Riddle: I am a number that is a multiple of both 3 and 5, and I come before 20. What number am I? |
|
Card: 14 / 50 |
Prime numbers are essential in mathematics because they serve as the building blocks of all natural numbers, allowing us to understand factors, multiples, and number theory. 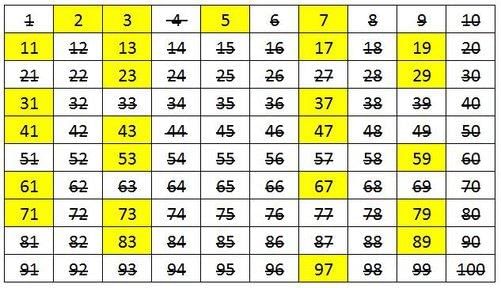 |
|
Card: 33 / 50 |
What happens if Jumpy chooses a number that is not a common factor of both treasures? |
|
Card: 37 / 50 |
A prime number is defined as a number greater than 1 that can only be divided evenly by ___ and ___ . |
|
Card: 42 / 50 |
A composite number has more than two factors, while a prime number has exactly two factors. |
|
Card: 45 / 50 |
Riddle: I am a number that can only be divided by 1 and myself, and I am greater than 1. What number am I? |
|
Card: 49 / 50 |
Using the Sieve of Eratosthenes, how would you identify prime numbers between 1 and 100? |
|
Card: 50 / 50 |
You eliminate all multiples of each prime starting from 2, leaving only prime numbers. |



























