|
A production function is a mathematical representation of the relationship between inputs (factors of production) and the maximum output that can be produced. It describes how different combinations of labor (L) and capital (K) can yield varying levels of output (q), expressed as q = f(L, K).  |
Card: 2 / 50 |
|
In the context of production functions, what are the differences between short-run and long-run production functions? |
Card: 3 / 50 |
|
In a short-run production function, some factors of production are fixed, leading to the application of the law of diminishing marginal product. In contrast, a long-run production function allows all factors to be variable, enabling the application of the law of returns to scale, which includes constant, increasing, and decreasing returns to scale.  |
Card: 4 / 50 |
|
Fill in the blank: The Cobb-Douglas production function is a specific example of a ___ function. |
Card: 5 / 50 |
|
True or False: The law of diminishing marginal product applies in the long run when all factors of production are variable. |
Card: 7 / 50 |
|
False. The law of diminishing marginal product applies in the short run when some factors are fixed. 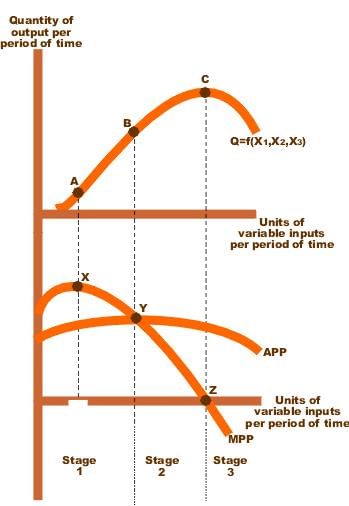 |
Card: 8 / 50 |
|
When technology improves, the maximum levels of output obtainable for different input combinations increase, resulting in a new production function that can produce more output from the same inputs. |
Card: 10 / 50 |
|
Riddle: I describe the relationship between inputs and output, and I'm often represented as a mathematical equation. What am I? |
Card: 11 / 50 |
|
Fill in the blank: The equation for a basic production function can be expressed as q = f(L, K), where q represents ___, L represents ___, and K represents ___. |
Card: 13 / 50 |
|
What are the types of returns to scale described in the long-run production function? |
Card: 15 / 50 |
|
The types of returns to scale are constant returns to scale (CRS), increasing returns to scale (IRS), and decreasing returns to scale (DRS). |
Card: 16 / 50 |
|
Factors of production, including labor (L) and capital (K), are essential inputs in the production process that determine the quantity and efficiency of output (q) that can be produced. The combination and management of these factors directly influence a firm's productivity and profitability. |
Card: 18 / 50 |
|
What does the production function tell us about the relationship between output and factors of production? |
Card: 19 / 50 |
|
The production function illustrates how different combinations of labor and capital can produce varying levels of output, helping to identify the most efficient input allocations for maximizing production. |
Card: 20 / 50 |
|
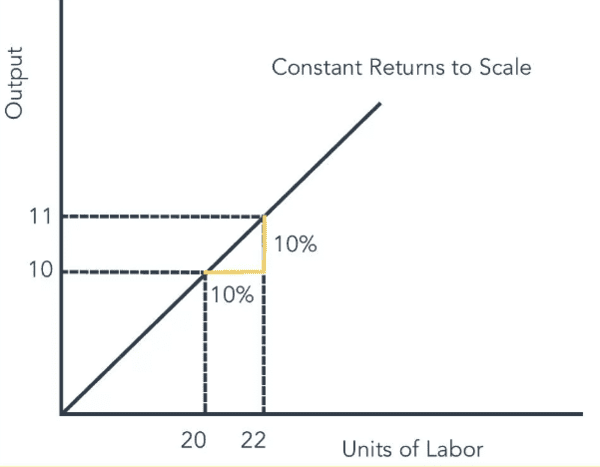
Constant Returns to Scale (CRS) occurs when ___ inputs are increased, resulting in an equal percentage increase in output. |
Card: 23 / 50 |
|
True or False: Increasing Returns to Scale (IRS) means that increasing all inputs results in a smaller percentage increase in output. |
Card: 25 / 50 |
 Unlock all Flashcards with EduRev Infinity Plan Starting from @ ₹99 only
|
|
False. Increasing Returns to Scale (IRS) means that increasing all inputs results in a greater percentage increase in output. |
Card: 26 / 50 |
|
Fill in the blanks: In the context of production functions, the output elasticities of labor and capital are represented by ___ and ___, respectively. |
Card: 27 / 50 |
|
What is the effect of Decreasing Returns to Scale (DRS) on output when all inputs are increased? |
Card: 29 / 50 |
|
Riddle: I can grow but not in size; I can change but not in form. What am I in the context of production functions? |
Card: 31 / 50 |
|
Total factor productivity (A) as it reflects efficiency rather than physical size. |
Card: 32 / 50 |
|
If total factor productivity increases, how does this affect the output in the function q = A * L^α * K^β? |
Card: 33 / 50 |
|
An increase in total factor productivity (A) leads to an increase in output (q) for the same levels of labor (L) and capital (K). |
Card: 34 / 50 |
|
In the function q = A * L^α * K^β, what happens to output if both labor and capital are doubled under Constant Returns to Scale? |
Card: 35 / 50 |
|
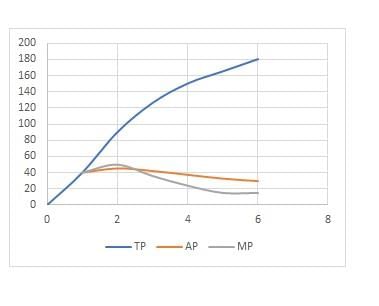
Total Product is defined as ___ produced by a firm using a specific amount of inputs over a certain period. |
Card: 37 / 50 |
|
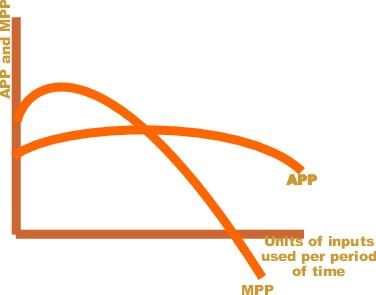
Fill in the blanks: When MP is greater than AP, AP ___; when MP is less than AP, AP ___. |
Card: 45 / 50 |
|
Riddle: I measure the change in output from an additional input, but I can become negative if too much is added. What am I? |
Card: 47 / 50 |
|
The relationship between Total Product, Average Product, and Marginal Product shows that when TP increases at a decreasing rate, MP ___ . |
Card: 49 / 50 |