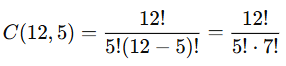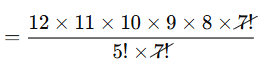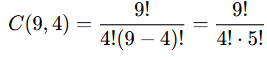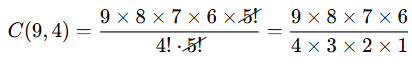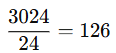|
A permutation is an arrangement of objects in a specific order. The number of permutations of n distinct objects taken r at a time is calculated using the formula |
Card: 2 / 24 |
|
What is the formula for the number of combinations of n distinct objects taken r at a time? |
Card: 3 / 24 |
|
The formula for combinations is |
Card: 4 / 24 |
|
If you have 7 different shirts and want to choose 4 to wear, how many different combinations can you make? |
Card: 5 / 24 |
|
Since 'APPLE' has 5 letters with the letter 'P' repeated twice, the arrangements can be calculated using the formula for arrangements of a multiset: 5! / (2!) = 60. Therefore, there are 60 distinct arrangements. |
Card: 8 / 24 |
|
A basketball team has 12 players. How many ways can a coach choose 5 players to start the game? |
Card: 9 / 24 |
|
Using the combination formula: |
Card: 10 / 24 |
|
The number of ways to arrange 5 distinct books is given by the permutation of all 5 books: P(5, 5) = 5! = 120. Therefore, there are 120 different arrangements. |
Card: 12 / 24 |
 Unlock all Flashcards with EduRev Infinity Plan Starting from @ ₹99 only
|
|
If a committee of 4 is to be formed from 9 members, how many different committees can be formed? |
Card: 13 / 24 |
|
Using the combination formula: |
Card: 14 / 24 |
|
The total arrangements of the letters in 'MISSISSIPPI' can be calculated using: |
Card: 16 / 24 |
|
What is a useful tip for solving permutation and combination problems quickly? |
Card: 17 / 24 |
|
A useful tip is to identify whether the order of selection matters (permutation) or not (combination). Also, for combinations, remember C(n, r) = C(n, n - r) which can simplify calculations. |
Card: 18 / 24 |
|
The number of ways to arrange 10 students in 10 chairs is |
Card: 20 / 24 |
|
How many ways can you select a president, vice president, and secretary from a group of 5 people? |
Card: 21 / 24 |
|
Since the order matters, this is a permutation problem: |
Card: 22 / 24 |
|
How many ways can you select 4 fruits from 10 different fruits if the selection order does not matter?
|
Card: 23 / 24 |
|
Using the combination formula: |
Card: 24 / 24 |





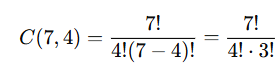
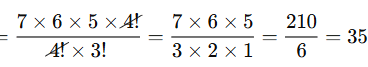 Thus, there are 35 ways to choose the shirts.
Thus, there are 35 ways to choose the shirts.