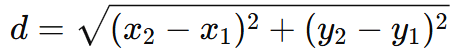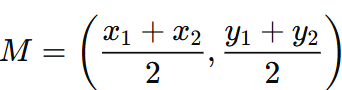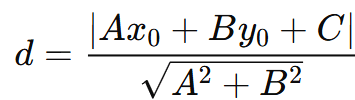What is the distance formula in coordinate geometry?

The distance formula is used to find the distance between two points (x1, y1) and (x2, y2) in a Cartesian plane. 
It is given by the formula: 

What is the midpoint formula for two points?

The midpoint formula calculates the midpoint M between two points (x₁, y₁) and (x₂, y₂) as

How do you determine the slope of a line given two points?

The slope of a line passing through two points (x₁, y₁) and (x₂, y₂) is calculated using the formula: 

m = (y₂ - y₁) / (x₂ - x₁).

Find the equation of a line with a slope of 2 that passes through the point (3, 4).

(Hint: Use the point-slope form of a line)

Using the point-slope form, 

y - y₁ = m(x - x₁), 
where m = 2, x₁ = 3, and y₁ = 4: 
y - 4 = 2(x - 3). 
Simplifying gives the equation: 
y = 2x - 2.

What is the relationship between the slopes of two perpendicular lines?

The slopes of two perpendicular lines are negative reciprocals of each other. If m₁ is the slope of the first line, and m₂ is the slope of the second line, 
then m₁ x m₂ = -1.

What is the equation of a circle with center (h, k) and radius r?

The equation of a circle with center (h, k) and radius r is given by 
(x - h)² + (y - k)² = r².

How do you find the equation of a line in slope-intercept form?

The slope-intercept form of a line is given by 
y = mx + b, 
where m is the slope and b is the y-intercept.

What is the formula for the area of a triangle formed by three points in the coordinate plane?

The area A of a triangle formed by points (x₁, y₁), (x₂, y₂), and (x₃, y₃) can be calculated using the formula: 

A = ½ |x₁(y₂ - y₃) + x₂(y₃ - y₁) + x₃(y₁ - y₂|

What is the standard form of a linear equation?

The standard form of a linear equation is Ax + By = C, where A, B, and C are integers, and A ≥ 0.

Determine the coordinates of the intersection of the lines y = 3x + 2 and y = -x + 4.

(Hint: Set the two equations equal to each other)

To find the intersection, set 3x + 2 = -x + 4. 

Solving gives x = ½. Substituting x back into either equation gives 

y = 3(½) + 2 = 3. 

The intersection point is
(½, 3).

What is the slope of a horizontal line?

The slope of a horizontal line is 0, as there is no change in the y-value regardless of the change in the x-value.

What is the slope of a vertical line?

The slope of a vertical line is undefined, as the x-value does not change while the y-value can vary.

If a line has a slope of 4 and passes through the origin, what is its equation?

The equation of the line is y = 4x, since it passes through the origin (0, 0), giving a y-intercept of 0.

What is the formula to find the distance from a point (x₀, y₀) to a line Ax + By + C = 0?

The distance d from point (x₀, y₀) to the line Ax + By + C = 0 is given by 

Find the length of the line segment between the points (2, 3) and (5, 7).

(Hint: Use the distance formula)

Using the distance formula, 
 d = √((5 - 2)² + (7 - 3)²) 
= √(3² + 4²) 
= √(9 + 16) 
= √25 
= 5.