Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > For continuous slab of 3m*3.5m size, the mini...
Start Learning for Free
For continuous slab of 3m*3.5m size, the minimum overall depth of slab to satisfy vertical deflection limit is?
Verified Answer
For continuous slab of 3m*3.5m size, the minimum overall depth of slab...
Ans.
Method to Solve :
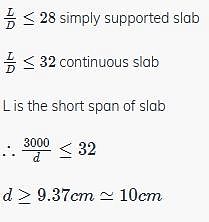
 This question is part of UPSC exam. View all Civil Engineering (CE) courses
This question is part of UPSC exam. View all Civil Engineering (CE) courses
Most Upvoted Answer
For continuous slab of 3m*3.5m size, the minimum overall depth of slab...
Introduction:
In order to determine the minimum overall depth of a continuous slab that satisfies the vertical deflection limit, several factors need to be considered. These factors include the material properties, loading conditions, and the deflection criteria specified for the slab.
Material properties:
The material properties of the slab, such as the modulus of elasticity (E) and the moment of inertia (I), will affect its deflection behavior. A higher modulus of elasticity and moment of inertia will result in a stiffer slab and lower deflections.
Loading conditions:
The loading conditions applied to the slab will play a significant role in determining its deflection. Different types of loads, such as dead loads (self-weight of the slab) and live loads (imposed loads), will have different effects on the deflection. It is important to consider the worst-case loading scenario that will result in the highest deflection.
Deflection criteria:
The specified vertical deflection limit for the slab will dictate the minimum overall depth required. This limit is usually expressed as a ratio of the deflection to the span length of the slab. For example, a common deflection limit is L/360, where L is the span length of the slab. This means that the maximum deflection should not exceed 1/360th of the span length.
Calculation of minimum overall depth:
To calculate the minimum overall depth of the slab, the deflection equation for a simply supported beam can be used. This equation relates the maximum deflection (δ) to the applied load (W), span length (L), material properties (E and I), and the slab depth (d):
δ = (W * L^3) / (48 * E * I)
Rearranging the equation to solve for the slab depth (d), we get:
d = ((W * L^3) / (48 * E * I))^(1/4)
By substituting the appropriate values for the applied load, span length, material properties, and the desired deflection limit, we can calculate the minimum overall depth of the slab.
Conclusion:
In conclusion, to determine the minimum overall depth of a continuous slab that satisfies the vertical deflection limit, it is necessary to consider the material properties, loading conditions, and the specified deflection criteria. By using the deflection equation and rearranging it to solve for the slab depth, the minimum overall depth can be calculated. It is important to ensure that the calculated depth satisfies the deflection limit to ensure the structural integrity and functionality of the slab.
In order to determine the minimum overall depth of a continuous slab that satisfies the vertical deflection limit, several factors need to be considered. These factors include the material properties, loading conditions, and the deflection criteria specified for the slab.
Material properties:
The material properties of the slab, such as the modulus of elasticity (E) and the moment of inertia (I), will affect its deflection behavior. A higher modulus of elasticity and moment of inertia will result in a stiffer slab and lower deflections.
Loading conditions:
The loading conditions applied to the slab will play a significant role in determining its deflection. Different types of loads, such as dead loads (self-weight of the slab) and live loads (imposed loads), will have different effects on the deflection. It is important to consider the worst-case loading scenario that will result in the highest deflection.
Deflection criteria:
The specified vertical deflection limit for the slab will dictate the minimum overall depth required. This limit is usually expressed as a ratio of the deflection to the span length of the slab. For example, a common deflection limit is L/360, where L is the span length of the slab. This means that the maximum deflection should not exceed 1/360th of the span length.
Calculation of minimum overall depth:
To calculate the minimum overall depth of the slab, the deflection equation for a simply supported beam can be used. This equation relates the maximum deflection (δ) to the applied load (W), span length (L), material properties (E and I), and the slab depth (d):
δ = (W * L^3) / (48 * E * I)
Rearranging the equation to solve for the slab depth (d), we get:
d = ((W * L^3) / (48 * E * I))^(1/4)
By substituting the appropriate values for the applied load, span length, material properties, and the desired deflection limit, we can calculate the minimum overall depth of the slab.
Conclusion:
In conclusion, to determine the minimum overall depth of a continuous slab that satisfies the vertical deflection limit, it is necessary to consider the material properties, loading conditions, and the specified deflection criteria. By using the deflection equation and rearranging it to solve for the slab depth, the minimum overall depth can be calculated. It is important to ensure that the calculated depth satisfies the deflection limit to ensure the structural integrity and functionality of the slab.
Attention Civil Engineering (CE) Students!
To make sure you are not studying endlessly, EduRev has designed Civil Engineering (CE) study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Civil Engineering (CE).

|
Explore Courses for Civil Engineering (CE) exam
|

|
Similar Civil Engineering (CE) Doubts
For continuous slab of 3m*3.5m size, the minimum overall depth of slab to satisfy vertical deflection limit is?
Question Description
For continuous slab of 3m*3.5m size, the minimum overall depth of slab to satisfy vertical deflection limit is? for Civil Engineering (CE) 2024 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about For continuous slab of 3m*3.5m size, the minimum overall depth of slab to satisfy vertical deflection limit is? covers all topics & solutions for Civil Engineering (CE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for For continuous slab of 3m*3.5m size, the minimum overall depth of slab to satisfy vertical deflection limit is?.
For continuous slab of 3m*3.5m size, the minimum overall depth of slab to satisfy vertical deflection limit is? for Civil Engineering (CE) 2024 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about For continuous slab of 3m*3.5m size, the minimum overall depth of slab to satisfy vertical deflection limit is? covers all topics & solutions for Civil Engineering (CE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for For continuous slab of 3m*3.5m size, the minimum overall depth of slab to satisfy vertical deflection limit is?.
Solutions for For continuous slab of 3m*3.5m size, the minimum overall depth of slab to satisfy vertical deflection limit is? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of For continuous slab of 3m*3.5m size, the minimum overall depth of slab to satisfy vertical deflection limit is? defined & explained in the simplest way possible. Besides giving the explanation of
For continuous slab of 3m*3.5m size, the minimum overall depth of slab to satisfy vertical deflection limit is?, a detailed solution for For continuous slab of 3m*3.5m size, the minimum overall depth of slab to satisfy vertical deflection limit is? has been provided alongside types of For continuous slab of 3m*3.5m size, the minimum overall depth of slab to satisfy vertical deflection limit is? theory, EduRev gives you an
ample number of questions to practice For continuous slab of 3m*3.5m size, the minimum overall depth of slab to satisfy vertical deflection limit is? tests, examples and also practice Civil Engineering (CE) tests.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.

























