Physics Exam > Physics Questions > A weightless piston divides a thermally insul...
Start Learning for Free
A weightless piston divides a thermally insulated cylinder into two parts of volumes V and 3V. 2 moles of an ideal gas at pressure P = 2 atmosphere are confined to the part with volume V = 1 litre. The remainder of the cylinder is evacuated. Initially the gas is at room temperature. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy (in Joule) in the process. The ratio of the specific heat of the gas γ = 1.5.
Correct answer is '400'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A weightless piston divides a thermally insulated cylinder into two pa...
As the expansion is against zero pressure, so no work is done. Now, for given mass of gas,
PV = P1V1
= P1 x 4V
∴ P1 = P/4 is the pressure of gas after expansion.
In the second process, compression is adiabatic, so
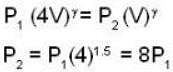
Change in internal energy = work done in adiabatic compression.
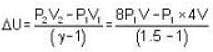
= 8P1V = 2PV
= 2 * 2 * 105 * 10-3 = 400J
Further,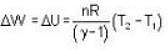
∴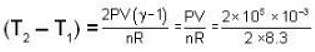
= 12.05
∴ Final temperature = T1 + (T2 - T2)
= 300 + 12.05 = 312.05 K
PV = P1V1
= P1 x 4V
∴ P1 = P/4 is the pressure of gas after expansion.
In the second process, compression is adiabatic, so
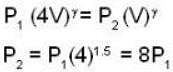
Change in internal energy = work done in adiabatic compression.
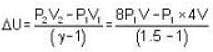
= 8P1V = 2PV
= 2 * 2 * 105 * 10-3 = 400J
Further,
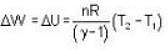
∴
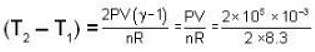
= 12.05
∴ Final temperature = T1 + (T2 - T2)
= 300 + 12.05 = 312.05 K
Most Upvoted Answer
A weightless piston divides a thermally insulated cylinder into two pa...
To solve this problem, we need to consider the fact that the process is adiabatic, meaning there is no heat exchange with the surroundings. Therefore, the change in internal energy of the gas is equal to the work done on or by the gas.
First, let's calculate the initial and final volumes of the gas.
Initial volume of the gas (V1) = 1 litre
Final volume of the gas (V2) = 3V + V = 4V
Next, let's calculate the work done on the gas when it expands.
Work done on the gas (W) = P * (V2 - V1)
= 2 atm * (4V - 1 litre)
Now, we need to find the value of V. To do this, we can use the ideal gas law.
PV = nRT
Since the gas is at room temperature, we can assume it is at 298 K.
Substituting the given values, we have:
2 atm * V = 2 moles * 0.0821 L.atm/(mol.K) * 298 K
V = 2 * 0.0821 * 298 / 2
V = 48.822 L
Now, we can substitute the value of V in the equation for work done:
W = 2 atm * (4 * 48.822 L - 1 litre)
W = 2 atm * (195.288 L - 1 litre)
W = 2 atm * 194.288 L
Finally, we can calculate the increase in internal energy (ΔU) using the first law of thermodynamics:
ΔU = W
Substituting the value of W, we have:
ΔU = 2 atm * 194.288 L
To convert this to Joules, we need to multiply by the conversion factor:
ΔU = 2 atm * 194.288 L * 101.325 J/(L.atm)
ΔU = 39361.56 J
Therefore, the increase in internal energy of the gas in this process is 39361.56 Joules.
First, let's calculate the initial and final volumes of the gas.
Initial volume of the gas (V1) = 1 litre
Final volume of the gas (V2) = 3V + V = 4V
Next, let's calculate the work done on the gas when it expands.
Work done on the gas (W) = P * (V2 - V1)
= 2 atm * (4V - 1 litre)
Now, we need to find the value of V. To do this, we can use the ideal gas law.
PV = nRT
Since the gas is at room temperature, we can assume it is at 298 K.
Substituting the given values, we have:
2 atm * V = 2 moles * 0.0821 L.atm/(mol.K) * 298 K
V = 2 * 0.0821 * 298 / 2
V = 48.822 L
Now, we can substitute the value of V in the equation for work done:
W = 2 atm * (4 * 48.822 L - 1 litre)
W = 2 atm * (195.288 L - 1 litre)
W = 2 atm * 194.288 L
Finally, we can calculate the increase in internal energy (ΔU) using the first law of thermodynamics:
ΔU = W
Substituting the value of W, we have:
ΔU = 2 atm * 194.288 L
To convert this to Joules, we need to multiply by the conversion factor:
ΔU = 2 atm * 194.288 L * 101.325 J/(L.atm)
ΔU = 39361.56 J
Therefore, the increase in internal energy of the gas in this process is 39361.56 Joules.

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
A weightless piston divides a thermally insulated cylinder into two parts of volumes V and 3V. 2 moles of an ideal gas at pressure P = 2 atmosphere are confined to the part with volume V = 1 litre. The remainder of the cylinder is evacuated. Initially the gas is at room temperature. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy (in Joule) in the process. The ratio of the specific heat of the gas γ = 1.5.Correct answer is '400'. Can you explain this answer?
Question Description
A weightless piston divides a thermally insulated cylinder into two parts of volumes V and 3V. 2 moles of an ideal gas at pressure P = 2 atmosphere are confined to the part with volume V = 1 litre. The remainder of the cylinder is evacuated. Initially the gas is at room temperature. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy (in Joule) in the process. The ratio of the specific heat of the gas γ = 1.5.Correct answer is '400'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A weightless piston divides a thermally insulated cylinder into two parts of volumes V and 3V. 2 moles of an ideal gas at pressure P = 2 atmosphere are confined to the part with volume V = 1 litre. The remainder of the cylinder is evacuated. Initially the gas is at room temperature. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy (in Joule) in the process. The ratio of the specific heat of the gas γ = 1.5.Correct answer is '400'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A weightless piston divides a thermally insulated cylinder into two parts of volumes V and 3V. 2 moles of an ideal gas at pressure P = 2 atmosphere are confined to the part with volume V = 1 litre. The remainder of the cylinder is evacuated. Initially the gas is at room temperature. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy (in Joule) in the process. The ratio of the specific heat of the gas γ = 1.5.Correct answer is '400'. Can you explain this answer?.
A weightless piston divides a thermally insulated cylinder into two parts of volumes V and 3V. 2 moles of an ideal gas at pressure P = 2 atmosphere are confined to the part with volume V = 1 litre. The remainder of the cylinder is evacuated. Initially the gas is at room temperature. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy (in Joule) in the process. The ratio of the specific heat of the gas γ = 1.5.Correct answer is '400'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A weightless piston divides a thermally insulated cylinder into two parts of volumes V and 3V. 2 moles of an ideal gas at pressure P = 2 atmosphere are confined to the part with volume V = 1 litre. The remainder of the cylinder is evacuated. Initially the gas is at room temperature. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy (in Joule) in the process. The ratio of the specific heat of the gas γ = 1.5.Correct answer is '400'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A weightless piston divides a thermally insulated cylinder into two parts of volumes V and 3V. 2 moles of an ideal gas at pressure P = 2 atmosphere are confined to the part with volume V = 1 litre. The remainder of the cylinder is evacuated. Initially the gas is at room temperature. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy (in Joule) in the process. The ratio of the specific heat of the gas γ = 1.5.Correct answer is '400'. Can you explain this answer?.
Solutions for A weightless piston divides a thermally insulated cylinder into two parts of volumes V and 3V. 2 moles of an ideal gas at pressure P = 2 atmosphere are confined to the part with volume V = 1 litre. The remainder of the cylinder is evacuated. Initially the gas is at room temperature. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy (in Joule) in the process. The ratio of the specific heat of the gas γ = 1.5.Correct answer is '400'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of A weightless piston divides a thermally insulated cylinder into two parts of volumes V and 3V. 2 moles of an ideal gas at pressure P = 2 atmosphere are confined to the part with volume V = 1 litre. The remainder of the cylinder is evacuated. Initially the gas is at room temperature. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy (in Joule) in the process. The ratio of the specific heat of the gas γ = 1.5.Correct answer is '400'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A weightless piston divides a thermally insulated cylinder into two parts of volumes V and 3V. 2 moles of an ideal gas at pressure P = 2 atmosphere are confined to the part with volume V = 1 litre. The remainder of the cylinder is evacuated. Initially the gas is at room temperature. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy (in Joule) in the process. The ratio of the specific heat of the gas γ = 1.5.Correct answer is '400'. Can you explain this answer?, a detailed solution for A weightless piston divides a thermally insulated cylinder into two parts of volumes V and 3V. 2 moles of an ideal gas at pressure P = 2 atmosphere are confined to the part with volume V = 1 litre. The remainder of the cylinder is evacuated. Initially the gas is at room temperature. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy (in Joule) in the process. The ratio of the specific heat of the gas γ = 1.5.Correct answer is '400'. Can you explain this answer? has been provided alongside types of A weightless piston divides a thermally insulated cylinder into two parts of volumes V and 3V. 2 moles of an ideal gas at pressure P = 2 atmosphere are confined to the part with volume V = 1 litre. The remainder of the cylinder is evacuated. Initially the gas is at room temperature. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy (in Joule) in the process. The ratio of the specific heat of the gas γ = 1.5.Correct answer is '400'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A weightless piston divides a thermally insulated cylinder into two parts of volumes V and 3V. 2 moles of an ideal gas at pressure P = 2 atmosphere are confined to the part with volume V = 1 litre. The remainder of the cylinder is evacuated. Initially the gas is at room temperature. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy (in Joule) in the process. The ratio of the specific heat of the gas γ = 1.5.Correct answer is '400'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















