Relations | RRB JE for Computer Science Engineering - Computer Science Engineering (CSE) PDF Download
- Relation or Binary relation R from set A to B is a subset of AxB which can be defined as:
aRb <=> (a,b) € R <=> R(a,b). - A Binary relation R on a single set A is defined as a subset of AxA. For two distinct sets, A and B with cardinalities m and n, the maximum cardinality of the relation R from A to B is mn.
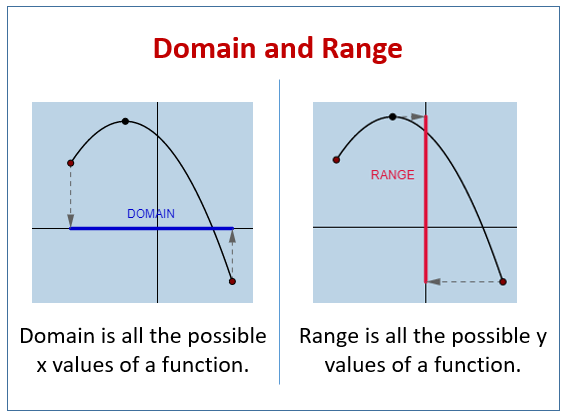
Domain and Range
- If there are two sets A and B and Relation from A to B is R(a,b), then the domain is defined as the set { a | (a,b) € R for some b in B}

- The range is defined as the set {b | (a,b) € R for some a in A}.
Example 1: State the domain and range of the following relation:
(eye colour, student's name).
A = {(blue,Steve), (green,Elaine), (brown,Kyle), (blue,Marsha), (brown,Miranda), (green, Dylan)}
State whether the relation is a function.
Solution: Domain: {blue, green, brown}. Range: {Steve, Elaine, Marsha, Miranda, Dylan}.
No, this relation is not a function. The eye colours are repeated.
Example 2: State the domain and range of the following relation: {(1,3), (-2,7), (3,-3), (4,5), (1,-3)}.
State whether the relation is a function.
Solution: Domain: {-2, 1, 3, 4}. Range: {-3, 3, 5, 7}.
While these listings appear in ascending order, the order is not required. Do not, however, duplicate an element.
No, this relation is not a function. The x-value of "1" had two corresponding y-values (3 and -3).
Types of Relation
- Empty Relation: A relation R on a set A is called Empty if set A is the empty set.
- Full Relation: A binary relation R on a set A and B is called full if AXB.
- Reflexive Relation: A relation R on a set A is called reflexive if (a,a) € R holds for every element a € A .i.e. if set A = {a,b} then R = {(a,a), (b,b)} is reflexive relation.
- Irreflexive relation : A relation R on a set A is called reflexive if no (a,a) € R holds for every element a € A.i.e. if set A = {a,b} then R = {(a,b), (b,a)} is irreflexive relation.
- Symmetric Relation: A relation R on a set A is called symmetric if (b,a) € R holds when (a,b) € R.i.e. The relation R={(4,5),(5,4),(6,5),(5,6)} on set A={4,5,6} is symmetric.
- AntiSymmetric Relation: A relation R on a set A is called antisymmetric if (a,b)€ R and (b,a) € R then a = b is called antisymmetric.i.e. The relation R = {(a,b)→R|a ≤ b} is anti-symmetric since a ≤ b and b ≤ a implies a = b.
- Transiitive Relation: A relation R on a set A is called transitive if (a,b) € R and (b,c) € R then (a,c) € R for all a,b,c € A.i.e. Relation R={(1,2),(2,3),(1,3)} on set A={1,2,3} is transitive.
- Equivalence Relation: A relation is an Equivalence Relation if it is reflexive, symmetric, and transitive. i.e. relation R={(1,1),(2,2),(3,3),(1,2),(2,1),(2,3),(3,2),(1,3),(3,1)} on set A={1,2,3} is equivalence relation as it is reflexive, symmetric, and transitive.
- Asymmetric relation: Asymmetric relation is the opposite of symmetric relation. A relation R on a set A is called asymmetric if no (b, a) € R when (a,b) € R.
Important Points
1. Symmetric and Anti-Symmetric relations are not opposite because a relation R can contain both the properties or may not.
2. A relation is asymmetric if and only if it is both anti-symmetric and irreflexive.
3. Number of different relations from a set with n elements to a set with m elements is 2mn
Example:
4. Number of Reflexive Relations on a set with n elements: 2n(n-1).
- A relation has ordered pairs (a,b). Now a can be chosen in n ways and same for b. So set of ordered pairs contains n2 pairs.
- Now for a reflexive relation, (a, a) must be present in these ordered pairs. And there will be total of n pairs of (a, a), so a number of ordered pairs will be n2-n pairs. So total number of reflexive relations is equal to 2n(n-1).
5. Number of Symmetric Relations on a set with n elements: 2n(n+1)/2.
- A relation has ordered pairs (a,b). Now for a symmetric relation, if (a,b) is present in R, then (b, a) must be present in R.
- In Matrix form, if a12 is present in relation, then a21 is also present in relation and As we know, reflexive relation is part of symmetric relation.
- So from total n2 pairs, only n(n+1)/2 pairs will be chosen for symmetric relation. So the total number of symmetric relations will be 2n(n+1)/2.
6. Number of Anti-Symmetric Relations on a set with n elements: 2n 3n(n-1)/2.
- A relation has ordered pairs (a,b). For anti-symmetric relation, if (a,b) and (b,a) is present in relation R, then a = b.(That means a is in relation with itself for any a).
So for (a, a), the total number of ordered pairs = n and the total number of relations = 2n. - If (a,b) and (b,a) both are not present in relation or Either (a,b) or (b,a) is not present in relation. So there are three possibilities and the total number of ordered pairs for this condition is n(n-1)/2. (selecting a pair is the same as selecting the two numbers from n without repetition) As we have to find a number of ordered pairs where a ≠ b.
- It is like opposite of symmetric relation means total number of ordered pairs = (n2) – symmetric ordered pairs(n(n+1)/2) = n(n-1)/2. So, total number of relation is 3n(n-1)/2. So total number of anti-symmetric relation is 2n.3n(n-1)/2.
7. Number of Asymmetric Relations on a set with n elements: 3n(n-1)/2.
- In Asymmetric Relations, element a can not be in relation with itself. (i.e. there is no aRa ∀ a∈A relation.) And then it is the same as Anti-Symmetric Relations. (i.e. you have three choices for pairs (a,b) (b, a)).
- Therefore there are 3n(n-1)/2 Asymmetric Relations possible.
8. Irreflexive Relations on a set with n elements : 2n(n-1).
- A relation has ordered pairs (a,b). For Irreflexive relation, no (a, a) holds for every element a in R. It is also the opposite of reflexive relation.
- Now for an Irreflexive relation, (a, a) must not be present in these ordered pairs means total n pairs of (a, a) are not present in R, So a number of ordered pairs will be n2-n pairs.
So total number of reflexive relations is equal to 2n(n-1).
9. Reflexive and Symmetric Relations on a set with n elements: 2n(n-1)/2.
- A relation has ordered pairs (a,b). Reflexive and symmetric Relations means (a,a) is included in R and (a,b)(b,a) pairs can be included or not. (In Symmetric relation for pair (a,b)(b,a) (considered as a pair).
- Whether it is included in relation or not) So a total number of Reflexive and symmetric Relations is 2n(n-1)/2.
|
12 videos|7 docs|103 tests
|
FAQs on Relations - RRB JE for Computer Science Engineering - Computer Science Engineering (CSE)
| 1. What is the domain and range of a relation? |  |
| 2. What are the different types of relations? |  |
| 3. What are the important points to consider in relations? |  |
| 4. How do relations relate to real-life situations? |  |
| 5. What are frequently asked questions about relations in exams? |  |
|
12 videos|7 docs|103 tests
|

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|