Addition in Binary | Mathematics for JAMB PDF Download
Binary addition is done by adding the digits starting from the right side of the numbers, in the same way as we add two or more base 10 numbers. In binary addition, the place values are given as ones, twos, fours, eights, sixteens, etc. We first add the digits in one's column, then we move towards the left, i.e., add the digits in the twos column, then the digits in the fours column, and so on. The only difference is that here we do regrouping when the sum of the digits becomes greater than 1.
What is Binary Addition?
Adding two or more binary numbers is one of the arithmetic operations on binary numbers or base-2 number systems. In decimal addition, when we add 3 + 2, we get 5. Similarly, when we add their binary equivalents, i.e (11)2 and (10)2, we get, (11)2 + (10)2 = (101)2, which is 5 in base-10. The results of both binary and decimal addition give us the same answer, the only difference is in the place values of the digits. The process of binary addition will look very familiar to you, the only difference is that in the decimal number system we regroup the next place value whenever we get the sum of the digits greater than 9 because in the decimal system we use 10 digits from 0 to 9. But while adding binary numbers, we regroup the next place value when the sum of the digits becomes greater than 1 as, in the binary number system, only two digits can be used, and those are 0 and 1.
Binary Addition Rules
The four rules that apply when two binary digits are added are given below:
Now, let us use these binary addition rules to learn the process of adding binary numbers.
Binary numbers are used in computers to store and represent data using digits 0 and 1. There are two cases that come up while learning about binary addition, and those are given below:
- Binary addition without regrouping
- Adding binary numbers with regrouping
Binary Addition without Regrouping
When the addition of two digits results in 0 or 1, then we don't need to regroup while adding two or more binary numbers. For example, let us add (101)2 and (10)2, which are the binary equivalents of 5 and 2 respectively.
Step 1: Write all the digits of both the numbers in separate columns as per their place values.
1 0 1
+ 1 0
-----------
-----------
Step 2: Start from the right-most column digits, 1 and 0. Apply one of the rules of binary addition which says 1 + 0 = 1.
1 0 1
+ 1 0
-----------
1
------------
Step 3: Move to the next column to the left. Here, we have two digits 0 and 1. Look at the rules given above and find out which rule will be applied here. Apply one of the binary addition rules which says 0 + 1 = 1.
1 0 1
+ 1 0
-----------
1 1
------------
Step 4: Now, in the last column, we have only 1 left, so we can apply the rule, 1 + 0 = 1.
1 0 1
+ 1 0
----------
1 1 1
----------
Therefore, by adding (101)2 with (10)2, we get (111)2 as the final answer.
Adding Binary Numbers with Regrouping
When the addition of two digits results in a number greater than 1, then we need to regroup while adding two or more binary numbers. For example, let us add (1001)2 and (111)2, which are the binary equivalents of 9 and 7 respectively.
- Step 1: Arrange the numbers as shown below.
- Step 2: Follow the binary addition rules to add the numbers. First let us add the digits in the one's place, which are 1 + 1 = 0 (1 carryover). Here, 1 + 1 is 10, which is the binary equivalent of (2)10, so we are regrouping the twos column by taking 1 as a carryover.
- Step 3: Now, we move to the next place value towards left, which is twos place. Here, we have 0 + 1 + 1 (carryover) = 10. So, again we will write 0 and take 1 as a carryover to the next place value. In the next column, we have 0 + 1 + 1 = 10. Similarly, we again take 1 as a carryover to the next column. In the last column to the left, we have 1 + 1 (carryover) = 10.
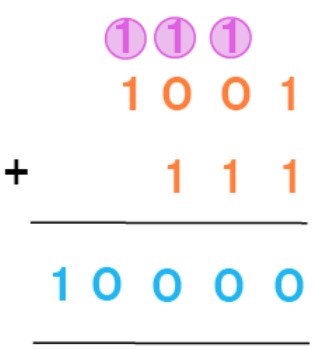
Therefore, (1001)2 + (111)2 = (10000)2.
Binary Addition Using 1's Complement
The 1's complement of a number can be found by interchanging every 0 to 1 and every 1 to 0 in a binary number. For example, the 1's complement of the binary number 110 is 001. Till now, we have studied adding all positive binary numbers but by using 1's complement, we can even add two negative binary numbers and one negative with a positive number.
First, let us learn how to add a positive number to a negative number. When the positive number is greater, we find the 1's complement of the negative number. Add the positive number and the 1's complement of the negative number. Then, we again add the end-around carry of the sum to the result to get the final answer. For example, let us add 1010 to (-1001). First, let us find 1's complement of the negative binary number, (-1001) by replacing 0 with 1 and 1 with 0. So, the 1's complement is 0110. Now we will add 0110 to the positive number which is 1010.
1 0 1 0
+ 0 1 1 0
-------------
1 0 0 0 0
-------------
Here, the end-around carry is 1, so we add it again to the rest of the number, which is 0000. Now, 0000+1 = 0001. So, 0001 is the answer when we add a positive number 1010 to a negative number (-1001).
When the negative number is greater than the positive number, then we first take the 1's complement of the negative number, then we add it to the positive number. Now, in this case, there will be no end-around carry. So, the final answer is obtained by taking the 1's complement of the resultant value. For example, to add 0111 and (-1000), we first find the 1's complement of -1000, which is 0111. Now, we add the 1's complement to the given positive binary number 0111.
0 1 1 1
+ 0 1 1 1
-------------
1 1 1 0
-------------
Now, find the 1's complement of 1110, which is 0001. Therefore, 0001 is the final answer after adding 0111 with -1000.
In the case of adding two negative binary numbers, first, we represent both the numbers in the 5-bit register by attaching the required number of zeros to the left. Then we find 1's complement of both the numbers and add the values. The end-around carry will be again added to the rest of the number. Note that in this case, we will always get a carryover digit. After adding, the 1's complement is to be found for the resultant number. That value with a negative sign will be the final answer.
For example, let us add two negative binary numbers -1010 and -0101. By representing both these numbers in the 5-bit register, we get 01010 and 00101. Now, we have to find 1's complement of both by replacing 1 with 0 and 0 with 1. We get 10101 and 11010 respectively. We get 101111 after adding both numbers. Here, 1 on the extreme left is the end-around carry and it will again be added to the rest of the number to its right (01111). Now, we have to find 1's complement of 10000, which is 01111. Hence, -01111 is the final answer.
|
139 videos|82 docs|101 tests
|


















