Surface Area of Adsorbent & Gibbs Adsorption Equation | Physical Chemistry PDF Download
11. Determination of Surface Area of the Adsorbent
Since the molar volume of an ideal gas at STP in 22.414 dm3, the number of molecules N adsorbed corresponding to the volume vmono is
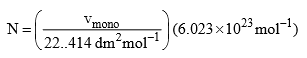
Where 6.023 × 1023 mol–1 is Avogadro constant. Now if the area of cross-section of a single molecule is known, it can be multiplied by the above number to give the total surface area of the adsorbent.
If ρ is the density, then the volume ν occupied by a single molecule (assuming the adsorbate to be highly packed with no void volume) is given by
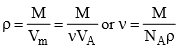
Assuming the molecule to be spherical, its cross-sectional area can be computed as follows. If r is the radius of the molecule, it follows that
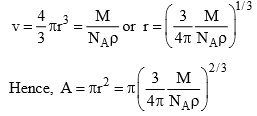
The obtained value of r (or πr2) is only an approximate value since it lacks the information regarding the exact nature of packing at the surface of the adsorbent. Even in the above method, the presence of void volume in the crystal lattice has been neglected. However, the latter can be accounted for provided crystal lattice of the solidified adsorbate is known.
Illustration: In adsorption of hydrogen over a sample of copper, monolayer-formation volume per gram of powder was found to be 1.36 cm3 measured at STP. Calculate the specific surface area of copper. Liquid hydrogen has a density of 0.07 g cm–3.
Solution: Number of molecule of hydrogen in 1.36 cm3 at STP is
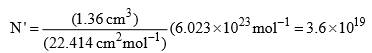
If liquid hydrogen is assumed to be closely packed (ignoring void volume), then the molar volume of hydrogen will be equal to NAν, where NA is Avogdro constant and ν is the volume of one molecule. If ρ is the density of liquid hydrogen, it is obvious that
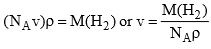
Substituting the value of M(H2), NA and ρ, we get
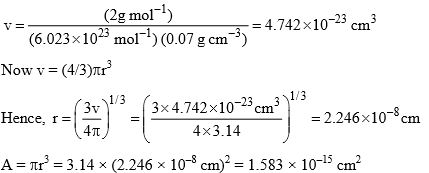
Specific area of copper = N’A = (3.6 × 1019) (1.583 × 10–15 cm2) = 5.70 × 104 cm2
12. Gibbs Adsorption Equation
The concentration of a solute at the surface of a solution may be different from that present in the bulk. The surface tension of a liquid, the surface tends to decrease its surface area in order to obtain a minimum value of surface free energy. The latter arises because of the unbalanced molecular forces experienced by the molecules at the surface. The surface tension is numerically equal to the surface energy per unit area of the surface. Now if the added solute has a surface tension lower than that of the liquid, then it has a tendency to accumulate more at the surface of the liquid since this way the surface tension of the liquid (or the surface free energy per unit area of the surface) is decreased. A quantitative expression which relates the excessive concentration of the solute at the surface (or the extent of adsorption) and the change in surface tension of the liquid (solvent) due to the addition of the solute was derived by J.W. Gibbs and is thus known as Gibbs adsorption equation. The latter can be derived as follows.
Following the additively, rule, the free energy of a system consisting of two components is given by G = n1μ1 + n2μ2 ………………………(1)
Where n1 and n2 are the amounts and μ1 and μ2 are the chemical potentials of the two components, respectively.
Since in the present case we are dealing with the change in the surface free energy, we must also add a factor corresponding to surface energy in eq. (1). If γ is the interfacial tension (or the interfacial energy per unit area) and s is the surface area, then the surface free energy is equal to γs. Thus eq. (1). In the present case, modifies, to
G = n1μ1 + n2μ2 + γs …………………..(2)
The complete differential of eq. (2) is given by
dG = n1dμ1 + n2dμ2 + μ2dn2 + γds + sdγ …………………..(3)
The function G will now depend on five independent variables, namely, T, p, n1, n2 and s, i.e.
G = f(T, p, n1, n2, s)
The total differential of G will be given by
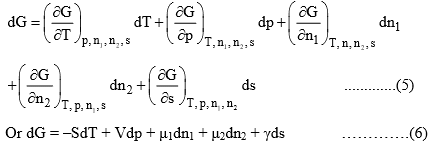
At constant temperature and pressure, eq. (6) reduces to

From eq. (7) and (3), we get
n1dμ1 + n2dμ2 + sdγ = 0 …………..(8)
The corresponding expression for the bulk of the liquid is

Where n01 and n02 are the respective amount of the liquid and solute in the bulk phase.
Now since the system is at equilibrium, the chemical potential of each of the components in both phases (surface and bulk) must be identical. When the system is slightly disturbed and it attains the new equilibrium, then the changes in chemical potential must be identical in both the phase, i.e., the differentials dμ1 and dμ2 in eq. (8) and (9) are identical. Eliminating dμ1 from these two equations, we get
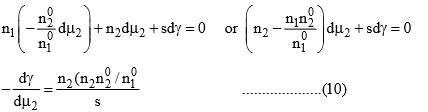
The expression within the bracket of eq. (10) gives the amount of solute that would be associated with the amount n1 of the liquid in the bulk phase. Since n2 is the amount of solute that is associated with the amount n1 of the liquid at the surface, the numerator on the right-hand side of eq. (10) gives the excessive amount of solute that is present in the surface of the liquid. Dividing this quantity with s gives the excess concentration of solute per unit area of surface. This quantity is represented by the symbol

Equation (11) is the required Gibbs adsorption equation. If we eliminate dμ2 instead of dμ2 instead to dμ1 from eqs. (8) and (9), we would have got the Gibbs adsorption equation as applicable to the liquid. It has a form

Where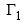 is the surface excessive concentration of the solvent at the surface of liquid.
is the surface excessive concentration of the solvent at the surface of liquid.
The chemical potential of the solute is given by
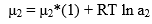
where μ2* (1) is the chemical potential of pure solute in liquid phase. Hence
dμ2 = RT d ln a2 ………………(13)
Substituting eq. (13) in eq. (11), we get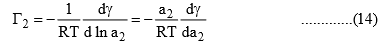
From a dilute solution, we have
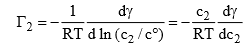 (where c0 issaturated unit concentration)
(where c0 issaturated unit concentration)
Example: According to Szyszkowski, the surface tension of an aqueous solution of butyric acid is related at 291 K to the bulk concentration c by the empirical relation.
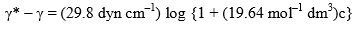
where γ* is the surface tension of pure water. Apply the Gibbs adsorption equation to calculate the excess concentration 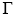 of solute per square centimeter of surface when c = 0.01 mol dm–3. What would be the value of
of solute per square centimeter of surface when c = 0.01 mol dm–3. What would be the value of 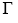 when c becomes infinite:
when c becomes infinite:
Solution: The Gibbs adsorption equation is 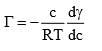
The expression of dγ/dc can be determined from the given empirical relation
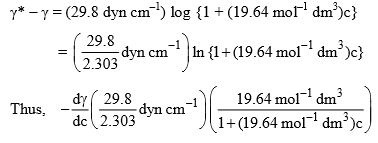
Hence, Eq. (1) becomes
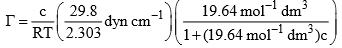
Substituting the given, data, we get
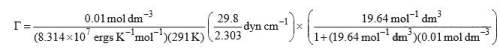
= 8.78 × 10–11 mol cm–2
The value of 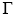 when c becomes infinite will be given by
when c becomes infinite will be given by
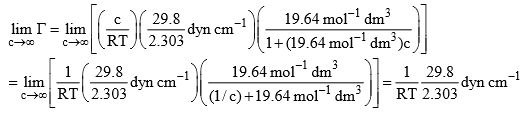
Thus, we have
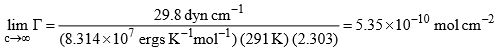
13. Surface-Active Substances
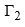 is positive if (dγ/dc2) is negative. In other words, if the surface tension of a solvent is decreased as a result of adding a solute, then the latter has relatively more concentration at the surface than in the bulk of the solutions. Substances which produce a marked reduction in surface tension are known as surface-active substances or surfactants. The limiting value of the decrease of surface tension with concentration, i.e., the quantity
is positive if (dγ/dc2) is negative. In other words, if the surface tension of a solvent is decreased as a result of adding a solute, then the latter has relatively more concentration at the surface than in the bulk of the solutions. Substances which produce a marked reduction in surface tension are known as surface-active substances or surfactants. The limiting value of the decrease of surface tension with concentration, i.e., the quantity 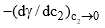 is called the surface activity.
is called the surface activity.
14. Surface-Inactive Substances
For surface-inactive substances dγ/dc is positive, i.e., an increase in the concentration of a surfaceinanctive substance in a solution causes an increase in the surface tension of the solution. From Gibbs equation, it follows that the value of  in such cases in negative indicating that the substance has larger concentration in the bulk in comparison to that present at the surface. This type of behaviour is known as negative adsorption. Examples include most of inorganic salts, sugar, etc.
in such cases in negative indicating that the substance has larger concentration in the bulk in comparison to that present at the surface. This type of behaviour is known as negative adsorption. Examples include most of inorganic salts, sugar, etc.
|
90 videos|144 docs|67 tests
|
FAQs on Surface Area of Adsorbent & Gibbs Adsorption Equation - Physical Chemistry
| 1. What is the surface area of an adsorbent and why is it important in adsorption processes? |  |
| 2. How is the surface area of an adsorbent determined experimentally? |  |
| 3. What is the Gibbs adsorption equation and how is it used in adsorption studies? |  |
| 4. How does the surface area of an adsorbent affect the adsorption capacity? |  |
| 5. Can the surface area of an adsorbent be modified or enhanced for specific adsorption applications? |  |

















