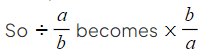Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Algebraic Fractions
Algebraic Fractions | Mathematics for GCSE/IGCSE - Class 10 PDF Download
Simplifying Algebraic Fractions
What is an algebraic fraction?
- An algebraic fraction is a fraction where the numerator and/or denominator contain algebraic expressions.
How do you simplify an algebraic fraction?
- Factorize both the numerator and denominator completely.
- Cancel out common factors, including those within brackets.
Adding & Subtracting Algebraic Fractions
How to Add (or Subtract) Algebraic Fractions
- The process for adding or subtracting algebraic fractions is akin to fractions with numbers.
- Finding the Lowest Common Denominator (LCD):
- The concept of finding the LCD between expressions like x - 2 and x + 5 involves multiplying them together. For instance, the LCD of x - 2 and x + 5 is (x - 2)(x + 5). This process is akin to determining the LCD of numbers, where, for example, the LCD of 2 and 9 is simply 2 x 9 = 18.
- Unlike the above scenario, when dealing with expressions like x and 2x, the LCD is not derived by multiplying them together. This is because 2x already incorporates an x, so the LCD in this case is simply 2x. Similarly, in the realm of numbers, the LCD of 2 and 4 is 4, not the product of 2 x 4, which is 8.
- When faced with expressions such as x - 2 and (x - 2)(x - 1), the LCD is simply (x - 2)(x - 1), as it already encompasses the term (x - 2). This mirrors the concept in numerical LCD calculations.
- Consider another scenario with expressions like x - 1 and (x - 1)^2. Here, the LCD simplifies to (x - 1)^2, as it already includes the term (x - 1).
- If confronted with (x - 3)(x - 1) and (x - 4)(x - 1), the LCD involves all three brackets: (x - 3)(x - 1)(x - 4), without repeating the (x - 1) element.
Steps for Working with LCD in Fractions
- Ensure each fraction is rewritten over the lowest common denominator.
- Multiply the numerators of each fraction by the same value as the denominators.
- Combine the fractions into a single one over the lowest common denominator by either adding or subtracting the numerators, remembering to use brackets when subtracting.
- Verify at the end if the numerator factorizes and cancels out.
Multiplying & Dividing Algebraic Fractions
How do I multiply algebraic fractions?
- Simplify both fractions by fully factorizing and canceling any common brackets on top or bottom.
- Multiply the numerators together.
- Multiply the denominators together.
- Check for any further factorizing and canceling if possible.
How do I divide algebraic fractions?
- Flip (reciprocate) the second fraction and replace ÷ with ×.
- Then follow the same rules for multiplying two fractions
The document Algebraic Fractions | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
38 videos|395 docs|19 tests
|
FAQs on Algebraic Fractions - Mathematics for GCSE/IGCSE - Class 10
| 1. What are the rules for multiplying algebraic fractions? |  |
Ans. When multiplying algebraic fractions, you simply multiply the numerators together and the denominators together. For example, (a/b) * (c/d) = ac/bd.
| 2. How do you factorize algebraic expressions when adding or subtracting algebraic fractions? |  |
Ans. To factorize algebraic expressions when adding or subtracting algebraic fractions, find the Lowest Common Denominator (LCD) and then rewrite the fractions with the LCD as the denominator.
| 3. Why is it important to leave fractions in factorized form when solving algebraic expressions? |  |
Ans. Leaving fractions in factorized form helps simplify the expression and make it easier to factorize, cancel out common factors, and find the LCD when adding or subtracting algebraic fractions.
| 4. Can algebraic fractions be simplified further after multiplying or dividing them? |  |
Ans. Yes, algebraic fractions can often be simplified further after multiplying or dividing by canceling out common factors in the numerator and denominator.
| 5. How do you find the LCD when adding or subtracting algebraic fractions? |  |
Ans. To find the LCD when adding or subtracting algebraic fractions, factorize the denominators and then multiply the highest power of each factor together to get the LCD.
Related Searches