Algebraic Identities | Mathematics (Maths) Class 9 PDF Download
What Are Algebraic Identities?
Algebraic identities are equations where the value on the left-hand side is always equal to the value on the right-hand side. Unlike regular algebraic expressions, these identities are true for all possible values of the variables involved.
You might remember that an algebraic identity is a type of equation that holds true for every value of its variables. Here are some common algebraic identities you have learned:
 Let us consider an example to understand this better. Consider the equations: 5x - 3 = 12, 10x - 6 = 24, and x2 + 5x + 6 = 0. These equations satisfy only a unit value and do not work for any other values of the variables.
Let us consider an example to understand this better. Consider the equations: 5x - 3 = 12, 10x - 6 = 24, and x2 + 5x + 6 = 0. These equations satisfy only a unit value and do not work for any other values of the variables.
Now let us consider an equation x2 - 9 = (x + 3)(x - 3). These equations satisfy any values of x.
From this, we can clearly understand that an algebra identity has an expression that satisfies any values for the variables. The basic algebraic identities are primarily helpful to work out the numerous math problems.
Standard Algebraic Identities List
All standard Algebraic Identities come from the Binomial Theorem, which is essential for understanding how to use them. The Binomial Theorem states that:
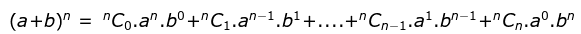
Some Standard Algebraic Identities list are given below:
Identity I: (a + b)2 = a2 + 2ab + b2
Identity II: (a – b)2 = a2 – 2ab + b2
Identity III: a2 – b2= (a + b)(a – b)
Identity IV: (x + a)(x + b) = x2 + (a + b) x + ab
Identity V: (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
Identity VI: (a + b)3 = a3 + b3 + 3ab (a + b)
Identity VII: (a – b)3 = a3 – b3 – 3ab (a – b)
Identity VIII: a3 + b3 + c3 – 3abc = (a + b + c)(a2 + b2 + c2 – ab – bc – ca)
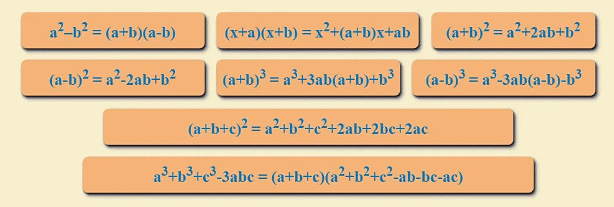
Example 1: Find the product of (x + 1)(x + 1) using standard algebraic identities.
Solution: (x + 1)(x + 1) can be written as (x + 1)2. Thus, it is of the form Identity I where a = x and b = 1. So we have,
(x + 1)2 = (x)2 + 2(x)(1) + (1)2 = x2 + 2x + 1
Example 2: Factorise (x4 – 1) using standard algebraic identities.
Solution: (x4 – 1) is of the form Identity III where a = x2 and b = 1. So we have,
(x4 – 1) = ((x2)2– 12) = (x2 + 1)(x2 – 1)
The factor (x2 – 1) can be further factorised using the same Identity III where a = x and b = 1. So,
(x4 – 1) = (x2 + 1)((x)2 –(1)2) = (x2 + 1)(x + 1)(x – 1)
Example 3: Factorise 16x2 + 4y2 + 9z2 – 16xy + 12yz – 24zx using standard algebraic identities.
Solution: 16x2 + 4y2 + 9z2– 16xy + 12yz – 24zx is of the form Identity V. So we have,
16x2 + 4y2 + 9z2 – 16xy + 12yz – 24zx = (4x)2 + (-2y)2 + (-3z)2 + 2(4x)(-2y) + 2(-2y)(-3z) + 2(-3z)(4x)= (4x – 2y – 3z)2 = (4x – 2y – 3z)(4x – 2y – 3z)
Example 4: Expand (3x – 4y)3 using standard algebraic identities.
Solution: (3x– 4y)3 is of the form Identity VII where a = 3x and b = 4y. So we have,
(3x – 4y)3 = (3x)3 – (4y)3– 3(3x)(4y)(3x – 4y) = 27x3 – 64y3 – 108x2y + 144xy2
Example 5: Factorize (x3 + 8y3 + 27z3 – 18xyz) using standard algebraic identities.
Solution: (x3 + 8y3 + 27z3 – 18xyz)is of the form Identity VIII where a = x, b = 2y and c = 3z. So we have,
(x3 + 8y3 + 27z3 – 18xyz) = (x)3 + (2y)3 + (3z)3 – 3(x)(2y)(3z)= (x + 2y + 3z)(x2 + 4y2 + 9z2 – 2xy – 6yz – 3zx)
Proof of Algebraic Identities
The following proofs of algebraic identities will help us to visually understand each of the identities and better understand it. Let us look at the proofs of each of the basic algebraic identities.
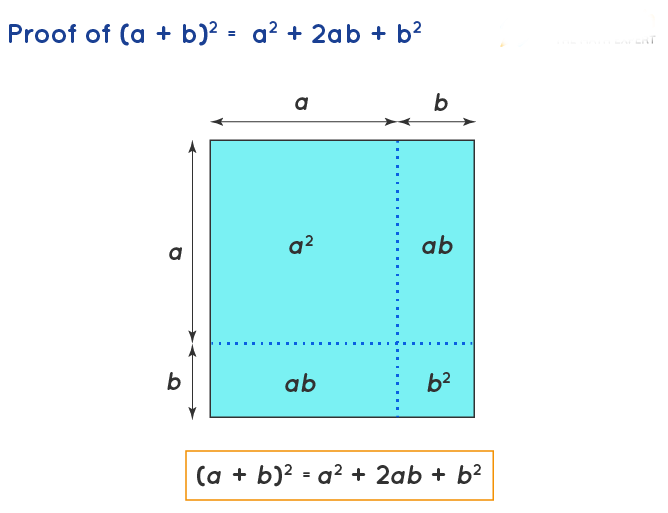
Identity I: Proof of (a + b)2 = a2 + 2ab + b2
- The algebraic expression (a+b)2 is nothing but (a+b) × (a+b).
- This can be visualized as a square whose sides are (a+b) and the area is (a+b)2.
- The square with a side of (a + b) can be visualized as four areas of a2, ab, ab, b2.
- The sum of these areas a2 + ab + ab + b2 gives the area of the square (a+b)2.
- The area of the square (a+b)2 = a2 + ab + ab + b2 proves the algebraic identity.
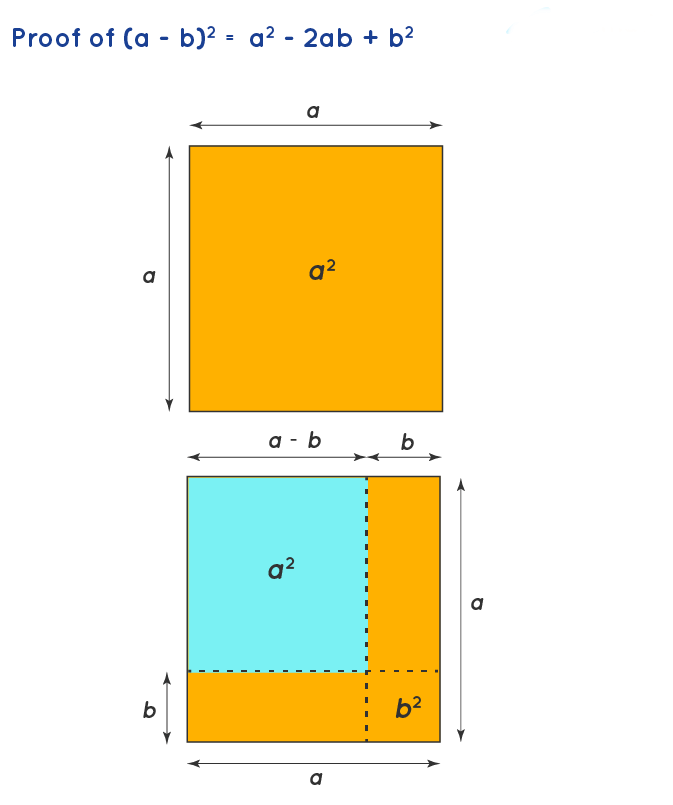
Identity II: Proof of (a − b)2 = a2 −2ab + b2
- Once again, let’s think of (a - b)2 as the area of a square with length (a - b).
- To understand this, let's begin with a large square of area a2.
- We need to reduce the length of all sides by b, and it becomes a - b.
- We now have to remove the extra bits from a2 to be left with (a - b)2.
- In the figure below, (a - b)2 is shown by the blue area.
- To get the blue square from the larger orange square, we have to subtract the vertical and horizontal strips that have the area ab.
- However, removing ab twice will also remove the overlapping square at the bottom right corner twice. Hence, we add b2.
- Thus we have (a − b)2 = a2 − ab − ab + b2.
- Hence this proves the algebraic identity (a − b)2 = a2 − 2ab + b2
Identity III: Proof of (a + b)(a - b) = a2 - b2
- The objective is to find the value a2 - b2, which can be taken as the difference of the area of two squares of sides a units and b units respectively.
- This is equal to the sum of are areas of two rectangles as presented in the below figure.
- One rectangle has a length of a units and a breadth of (a - b) units. Another rectangle is taken with a length of (a - b) and a breadth of b units.
- Further, we take the areas of the two rectangles and sum the areas to obtain the resultant values.
- The respective areas of the two rectangles are (a - b) × a = a(a - b) , and (a - b) × b = b(a - b).
- Finally, we take the sum of these areas to obtain the resultant expression.
- a(a + b) + b(a - b) = (a + b)(a - b)
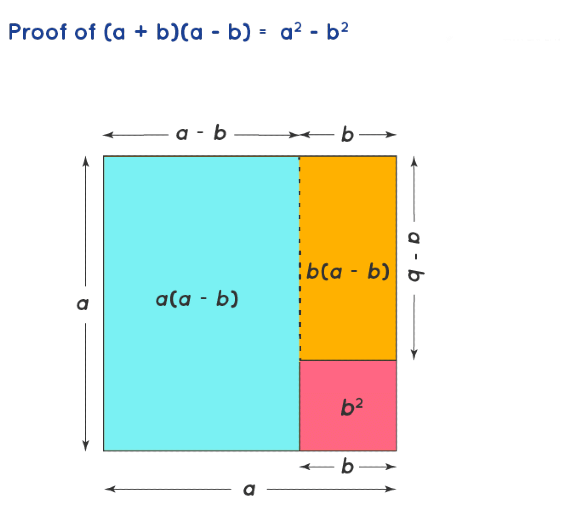
Re-arranging the individual squares and rectangles, we get:
(a+b)(a−b)=a2−b2
Identity IV: Proof of (x + a)(x + b) = x2 + x(a + b) + ab
- (x+a)(x+b) is nothing but the area of a rectangle whose sides are (x+a) and (x+b) respectively.
- The area of a rectangle with sides (x+a) and (x+b) in terms of the individual areas of the rectangles and the square is x2, ax, bx , ab.
- Summing all these areas we have x2 + ax + bx + ab.
- This gives us the proof for the algebra identity (x + a)(x + b) = x2 + ax + bx + ab = x2 + x(a + b) + ab.
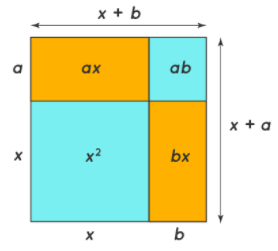 Proof of (x+a)(x+b)
Proof of (x+a)(x+b)
Identity V: (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
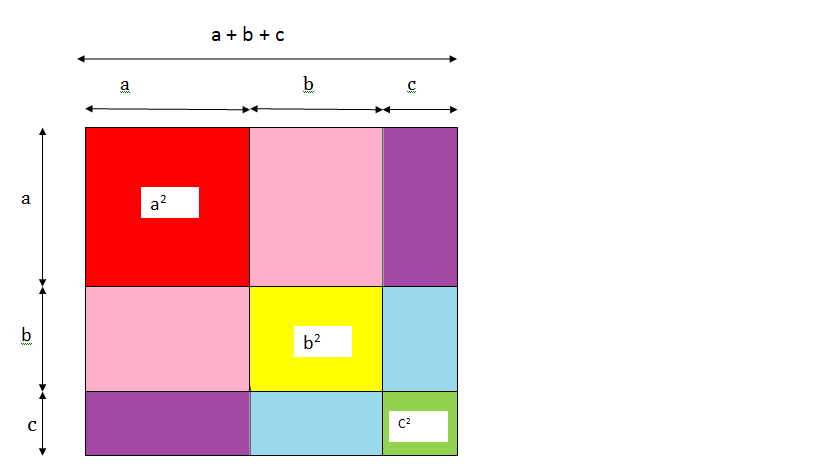
- Draw a square and cut into 9 parts.
- There are 3 squares (red, yellow, green) and 6 rectangles (2 pink, 2 purple, 2 blue)
- Area of the full square = (a + b + c)2
- Now we have to find the area of 3 inside square(red, yellow, green) = a2 + b2 + c2
- Consider the area of 2 pink rectangle = length × breadth = b.a + b.a = 2ab
- Area of 2 purple rectangle = a.c + a.c = 2ac and Area of 2 blue rectangle = b.c + b.c = 2bc
- Area of full square = area of 3 inside square + area of 2 pink rectangle + area of 2 purple rectangle + area of 2 blue rectangle.
i.e., (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ac
Hence, geometrically we proved the identity (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ac
Identity VI: (a + b)3 = a3 + b3 + 3ab (a + b)
Lets draw a cube with side length (a + b) , hence we know that the volume of this cube would be equal to (a + b)3

- Note that in the above diagram, the red part itself is a cube with volume a3 and the blue part is a cube with volume b3
- Further more, note that the yellow part is a cuboid with height a, width a, and length b ; thus the cuboid has volume a x a x b = a²b, and as the diagram has 3 yellow cuboids, the total volume of the yellow part would be 3a²b
- Similarly, the green part is a cuboid with height b, length b, and width a ; thus a cuboid with volume ab², and as the diagram has 3 green cuboids, the total volume of the green part is 3ab²
- We first remove the primary a3 cube and b3 from the image as shown below:
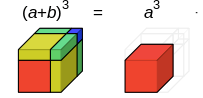
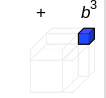
- Further evaluating the diagram allows us to remove other inscribed combination of shapes :
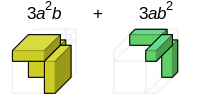
Identity VII: (a – b)3 = a3 – b3 – 3ab (a – b)
To prove the identity (a-b)3 = a3 - b3 - 3ab(a-b), let's consider a cube with side a and a smaller segment of side b:
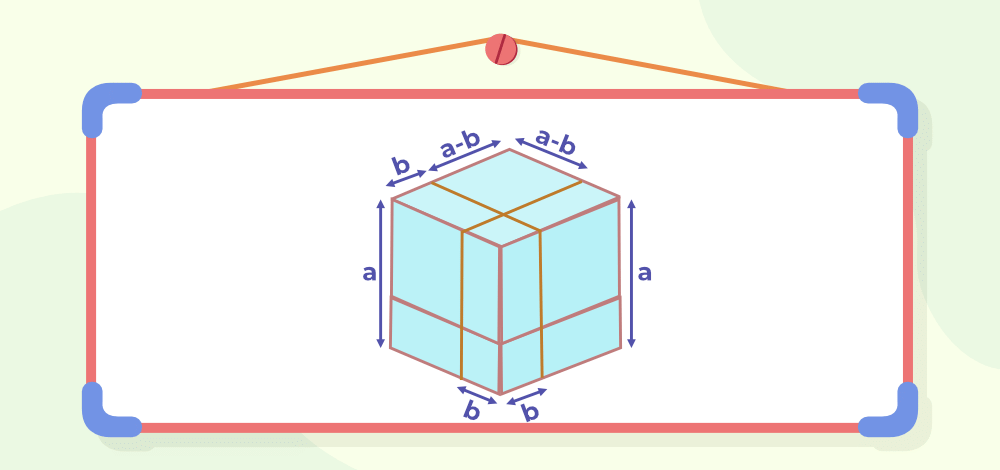
We can break the cubes into smaller sections to easily calculate volume as follows:
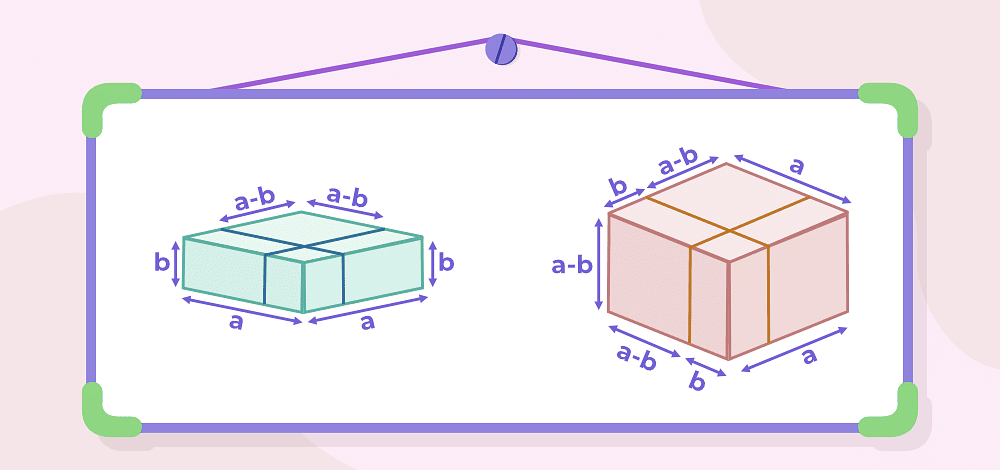
And further splitting these shapes into simpler cuboids and cubes:
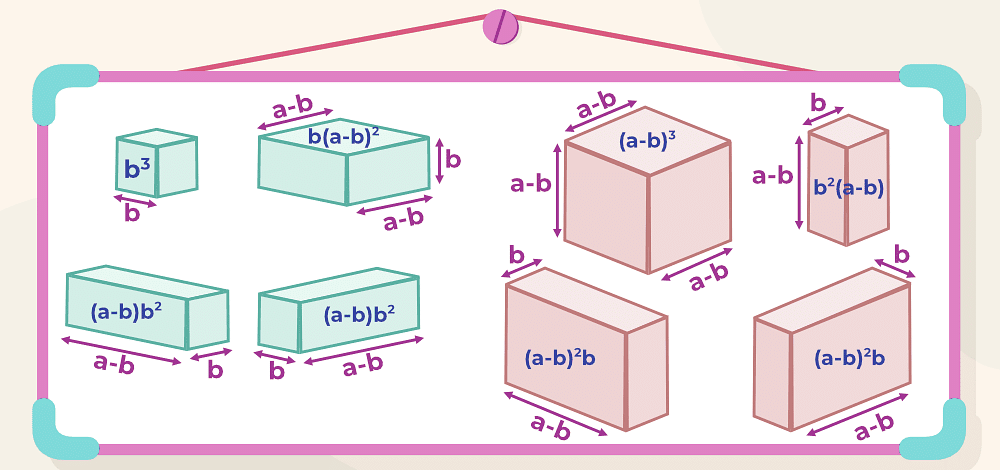
Now, we use the principle that volume remains constant before and after the transformations.
a3 = (a-b)3 + b2(a-b) + (a-b)2b + (a-b)2b + b3 + (a-b)2b + (a-b)b2 + (a-b)b2
⇒ a3 = (a-b)3 + b(a-b)[b + a - b + a - b + b + b] + b3
⇒ a3 = (a-b)3 + b(a-b)[3a] + b3
⇒ a3 = (a-b)3 + 3ab(a-b) + b3
Rearranging gives us (a-b)3 = a3 - b3 - 3ab(a-b).
Thus, we have proven the identity (a-b)3 = a3 - b3 - 3ab(a-b).
Identity VIII: (x + y + z)(x 2 + y 2 + z 2 – xy – yz – zx)
On expanding, we get the product as
x(x 2 + y 2 + z 2 – xy – yz – zx)
+ y(x 2 + y 2 + z 2 – xy – yz – zx)
+ z(x 2 + y 2 + z 2 – xy – yz – zx)
= x 3 + xy2 + xz 2 – x 2y – xyz – zx2 + x 2y + y 3 + yz2 – xy2 – y 2 z – xyz + x 2 z + y 2 z + z 3 – xyz – yz2 – xz2
= x 3 + y 3 + z 3 – 3xyz (On simplification)
|
40 videos|471 docs|57 tests
|
FAQs on Algebraic Identities - Mathematics (Maths) Class 9
| 1. What are some common examples of algebraic identities? |  |
| 2. How are algebraic identities useful in solving algebraic equations? |  |
| 3. Can you provide a proof of algebraic identities? |  |
| 4. How can algebraic identities be applied in real-life situations? |  |
| 5. What is the importance of understanding algebraic identities in mathematics? |  |





















