Algebraic Identities | Advance Learner Course: Mathematics (Maths) Class 8 PDF Download
Algebraic Identities
The algebraic equations which are valid for all values of variables in them are called algebraic identities. They are also used for the factorization of polynomials. In this way, algebraic identities are used in the computation of algebraic expressions and solving different polynomials. You have already learned about a few of them in the junior grades. In this article, we will recall them and introduce you to some more standard algebraic identities, along with examples.
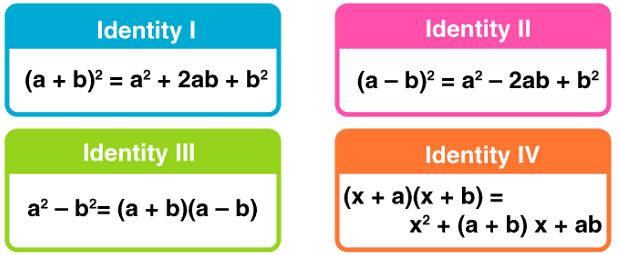
Standard Algebraic Identities List
All the standard Algebraic Identities are derived from the Binomial Theorem, which is given as:
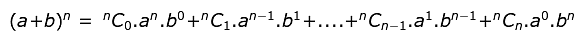
Some Standard Algebraic Identities list are given below:
Identity I: (a + b)2 = a2 + 2ab + b2
Identity II: (a – b)2 = a2 – 2ab + b2
Identity III: a2 – b2= (a + b)(a – b)
Identity IV: (x + a)(x + b) = x2 + (a + b) x + ab
Identity V: (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
Identity VI: (a + b)3 = a3 + b3 + 3ab (a + b)
Identity VII: (a – b)3 = a3 – b3 – 3ab (a – b)
Identity VIII: a3 + b3 + c3 – 3abc = (a + b + c)(a2 + b2 + c2 – ab – bc – ca)
Example 1: Find the product of (x + 1)(x + 1) using standard algebraic identities.
Solution: (x + 1)(x + 1) can be written as (x + 1)2. Thus, it is of the form Identity I where a = x and b = 1. So we have,
(x + 1)2 = (x)2 + 2(x)(1) + (1)2 = x2 + 2x + 1
Example 2: Factorise (x4 – 1) using standard algebraic identities.
Solution: (x4 – 1) is of the form Identity III where a = x2 and b = 1. So we have,
(x4 – 1) = ((x2)2– 12) = (x2 + 1)(x2 – 1)
The factor (x2 – 1) can be further factorised using the same Identity III where a = x and b = 1. So,
(x4 – 1) = (x2 + 1)((x)2 –(1)2) = (x2 + 1)(x + 1)(x – 1)
Eample 3: Factorise 16x2 + 4y2 + 9z2 – 16xy + 12yz – 24zx using standard algebraic identities.
Solution: 16x2 + 4y2 + 9z2– 16xy + 12yz – 24zx is of the form Identity V. So we have,
16x2 + 4y2 + 9z2 – 16xy + 12yz – 24zx = (4x)2 + (-2y)2 + (-3z)2 + 2(4x)(-2y) + 2(-2y)(-3z) + 2(-3z)(4x)= (4x – 2y – 3z)2 = (4x – 2y – 3z)(4x – 2y – 3z)
Example 4: Expand (3x – 4y)3 using standard algebraic identities.
Solution: (3x– 4y)3 is of the form Identity VII where a = 3x and b = 4y. So we have,
(3x – 4y)3 = (3x)3 – (4y)3– 3(3x)(4y)(3x – 4y) = 27x3 – 64y3 – 108x2y + 144xy2
Example 5: Factorize (x3 + 8y3 + 27z3 – 18xyz) using standard algebraic identities.
Solution: (x3 + 8y3 + 27z3 – 18xyz)is of the form Identity VIII where a = x, b = 2y and c = 3z. So we have,
(x3 + 8y3 + 27z3 – 18xyz) = (x)3 + (2y)3 + (3z)3 – 3(x)(2y)(3z)= (x + 2y + 3z)(x2 + 4y2 + 9z2 – 2xy – 6yz – 3zx)
|
5 videos|57 docs|20 tests
|
FAQs on Algebraic Identities - Advance Learner Course: Mathematics (Maths) Class 8
| 1. What is the Remainder Theorem in algebra? |  |
| 2. How can the Remainder Theorem be applied to find remainders? |  |
| 3. Can the Remainder Theorem be used to find factors of a polynomial? |  |
| 4. What is the relationship between the Remainder Theorem and the Factor Theorem? |  |
| 5. Can the Remainder Theorem be used to solve polynomial equations? |  |
|
5 videos|57 docs|20 tests
|

|
Explore Courses for Class 8 exam
|

|

















