Alphabet - 1 | IBPS PO Prelims & Mains Preparation - Bank Exams PDF Download
| Table of contents |
|
| Introduction |
|
| Code Based on English Alphabet |
|
| Rules to Solve |
|
| Rule 1 |
|
| Rule 2 |
|
| Rule 3 |
|
| Rule 4 |
|
| Rule 5 |
|
| Rule 6 |
|
Introduction
The reasoning section of every competitive exam is very crucial for an individual. This section can make or break the exam results for many students. There are many topics in the reasoning section and today we are going to cover one of those topics, Alphabetical Order. Generally, this topic covers adequate questions in the competitive exams and that is why it is a very important topic.
- All the test papers of reasoning in the competitive examinations start with a question based on ‘Alphabet’. Depending on the type and selection criteria, the number of questions vary. The understanding of English Alphabet is also essential to solve questions found in Coding-Decoding, Classification and Series.
- To solve the questions based on alphabets, one should remember the position of the alphabet from either side. Usually, a number of words are given in the series which individually are called the terms and there is a definite relationship between each term.
- The candidate should be able to recall the position of the alphabet fast enough to solve these problems and know the position not only from the left but from right as well.
Code Based on English Alphabet
- To solve questions pertaining to code based on the English alphabet, you must know the position of each letter from either end so that you can recognize the coding pattern quickly.
Table: Position of Alphabets From Left to Right
Table: Position of Alphabets From Right to Left
To memorise the position from left, the student should first learn the EJOTY Principle as explained here.
Each letter in the term EJOTY represents the position, which is a multiple of 5.
Rules to Solve
To solve questions based on alphabets, use the following rules:
Rule 1
To find the position of alphabet from L.H.S / R.H.S.
Directions (1-4): In the alphabet series we are given the position of an alphabet from L.H.S. What is the position of the alphabet from R.H.S.?Ex. 1: J is 10th alphabet from left.
Ex. 2: H is 8th alphabet from left.
Ex. 3: L is 12th alphabet from left.
Ex. 4: X is 24th alphabet from left.
Ans. 1: 27 – 10 = 17th from RHS.
Ans. 2: 27 – 8 = 19th from RHS.
Ans. 3: 27 – 12 = 15th from RHS.
Ans. 4: 27 – 24 = 3rd from RHS.
Similarly, if the position of an alphabet from right is known and we are required to find out its position from left, then just subtract the given position from 27 and we get the position of the alphabet from left.
T is 20th alphabet from left.
Directions (5-8): In the alphabet series we are given the position of an alphabet from R.H.S. What is the position of the alphabet from L.H.S.?Ex. 5: An alphabet is 14th from right.
Ex. 6: An alphabet is 2nd from right.
Ex. 7: An alphabet is 22nd from right.
Ex. 8: An alphabet is 9th from right.
Ans. 5: 27 – 14 = 13th from left.
Ans. 6: 27 – 2 = 25th from left.
Ans. 7: 27 – 22 = 5th from left.
Ans. 8: 27 – 9 = 18th from left.
An alphabet is 17th from right.
Rule 2
To find the opposite letter.
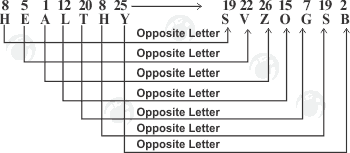
- When the sum of the position of two alphabets is 27, then these two words are opposite to each other in the series. A is the first letter and Z is its opposite in the series. Their respective positions are 1 and 26. The sum of their position is 1 + 26 = 27. As such both these letters are opposite to each other in the alphabet.
- To find out the alphabet, which is its opposite in the series, just subtract the place value of given alphabet from 27 and whatever we get the number, just find the alphabet regarding that place value, which is our answer.
Following are some examples to find out the opposite alphabet:
Ex. 9: Opposite letter of D?
Ex. 10: Opposite letter of V?
Ex. 11: Opposite letter of J?
Ex. 12: Opposite letter of S?
Ans. 10: V is 22nd letter in the series from LHS. So its opposite letter is 27 – 22= 5 i.e. E
Ans. 11: J is the 10th letter in the series from LHS. So its opposite letter is 27 – 10 = 17 i.e. Q
Ans. 12: S is 19th letter in the series from LHS. So its opposite letter is 27 – 19 = 8 i.e. H
Rule 3
To find the middle position between the two alphabets.
There are three cases under Rule 3
Case I (Rule 3)
When we are given the positions of the alphabets from left as well as from right in the alphabet series.
- Sometimes, the problem is to find out the alphabet which is in the middle of two given positions, i.e. from left and right. To the position given from right, add a particular number x so that the sum table is 27.
- Now, add that particular number x to the position from left. The sum total now around is divided by 2 to find out the position of the alphabet, which is in the middle of two given positions.
Following are the examples to find out the middle position of two alphabets:Ex. 13: 4th from right and 7th from left?
Ex. 14: 17th from left and 6th from right?
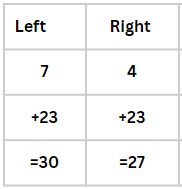
30/2 = 15 i.e. O
Ans. 14: We are required to find out the ‘middle’ letter between the 17th alphabet from left and the 6th alphabet from the right. The letter, which is 6th from right is 27-6= 21st from left. Adding both the left hand side positions, we get 17+21=38 and when we divide 38 by 2, the answer is 19.
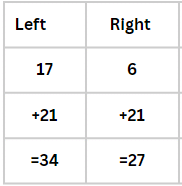
38/2 = 19 i.e. S
Which letter will be the midway between the fourteenth letter from the left end and nineteenth letter from the right end of the following alphabet ?
Case II (Rule 3)
When we are given only two alphabets.
- Sometimes we are given simply two alphabets then as we know the place values of these two alphabets, we simply add the place values of these alphabets and then divide the result by 2 to get the answer, i.e. the middle position of the alphabets.
Following are the examples to find out the middle position of two alphabets in this case:
Ex. 15: Which is the middle letter between H and N?
Ans:
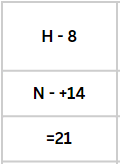
22/2 = 11 i.e. K
Ex. 16: Which is the middle letter between H and T?
28/2 = 14 i.e. N
Case III (Rule 3)
When we are given the position of two alphabets from R.H.S.
- In this case, we simply added the place values of alphabets and then divide the result by 2 as such in case 2.
- But here the answer we now get that is from R.H.S, but we need the answer from L.H.S. So, according to the rule 1, we simply subtract the above answer from 27 to get the answer from L.H.S.
Ex. 17: 10th from right and 4th from right
Rule 4
Relative position between the two alphabets.
- The first step is to find out from which side of the alphabet series are we to find the required alphabet, from the left side or the right side.
- The second step is to which side are we to look further; towards left or right. If we are looking for an alphabet from the left side of the series and the required one is to its right, then we add the right position to the position from left and if it is to its left, then we subtract from it.
General Pattern: Which alphabet is – to the left/ right of – from left/ right
So for this, we can make the following as the general rule:
Following are some of the examples:
Ex. 18: Which alphabet is 8th to right of 10th from left?
Ex. 19: Which alphabet is 4th to left of 20th from right?
Ans. 18: One position is from left and the other is from the right. So according to the above table:
8 + 10 = 18th from left i.e. R
Ans. 19: One position is from left and the other is from the right. So according to the above table:
4 + 20 = 24th from right = 3rd from left (27 – 24) i.e. C.
Rule 5
Arrangement of letters in alphabetical order and finding out the position from left or right.
- In this Rule, You must know the sequence of the alphabets by heart. So, you have to memorize the place values of alphabets so that you can arrange the letters of the given word in alphabetical order very quickly.
Following are some of the examples:
Ex. 20: If the word PENCIL is written alphabetically then which is the fourth letter from right?
Ex. 21: If the word COUNTER is written alphabetically then which is the third letter from left?
Ex. 22: If the word REPRESENTATION is written alphabetically then which is the second word to the left of fifth from right?
Ans. 20: PENCIL word when broken down can be written as CEILNP. So the fourth alphabet from right is I.
Ans. 21: The said letter after it is written in alphabetical order is: CENORTU. So the third letter from left is N.
Ans. 22: The said word after it is written in alphabetical order is: AEEEINNOPRRSTT. The second word to left of fifth from right is 5th + 2nd = 7th from right i.e. O.
Rule 6
Arrangement of words in alphabetical order.
- We know that in a dictionary, the words are arranged in alphabetical order. Therefore, you must know the basics of “Dictionary Usage”. The words beginning with the same letter of the English alphabet are again arranged in alphabetical order with respect to the second letter of words and so on.
Ex. 23: Arrange the following words in alphabetical order or as per the dictionary.
(a) Plight
(b) Pledge
(c) Pugilist
(d)PanderThe correct answer is (i) Pander (ii) Pledge (iii) Plight (iv) Pugilist
Ex. 24: Arrange the following words in alphabetical order or as per the dictionary.
(a) sundry
(b) script
(c) season
(d)slightThe correct answer is (i) Script (ii) Season (iii) slight (iv) Sundry
|
541 videos|683 docs|263 tests
|
FAQs on Alphabet - 1 - IBPS PO Prelims & Mains Preparation - Bank Exams
| 1. What is the significance of the English alphabet in coding for SSC CGL exams? |  |
| 2. What are some common rules used in coding based on the English alphabet for SSC CGL? | |
| 3. How can I practice coding questions for the SSC CGL exam? | |
| 4. Are there any specific strategies to solve coding questions in the SSC CGL exam? | |
| 5. How important are coding and decoding questions in the SSC CGL exam? | |
|
30.7K Views |
|
4.83/5 Rating |
|
Dec 22, 2024 Last updated |
|
541 videos|683 docs|263 tests
|
|
Explore Courses for Bank Exams exam
|
|
Viva Questions
,Alphabet - 1 | IBPS PO Prelims & Mains Preparation - Bank Exams
,practice quizzes
,shortcuts and tricks
,Alphabet - 1 | IBPS PO Prelims & Mains Preparation - Bank Exams
,ppt
,Semester Notes
,Alphabet - 1 | IBPS PO Prelims & Mains Preparation - Bank Exams
,Free
,study material
,Summary
,Extra Questions
,Sample Paper
,mock tests for examination
,video lectures
,Exam
,MCQs
,Previous Year Questions with Solutions
,past year papers
,Objective type Questions
,Important questions
;
Alphabet - 1 Free PDF Download
Importance of Alphabet - 1
Alphabet - 1 Notes
Alphabet - 1 Bank Exams Questions
Study Alphabet - 1 on the App
|
© EduRev
|
Education Revolution
|
|
