Angle Between Two lines | Mathematics (Maths) Class 11 - Commerce PDF Download
E. Angle Between Two Straight Lines
Ifθ is the acute angle between two lines, then  where m1 and m2 are the slopes of the two lines and are finite.
where m1 and m2 are the slopes of the two lines and are finite.

Notes :
(i) If the two lines are perpendicular to each other then m1m2 = -1
(ii) Any line perpendicular to ax + by + c = 0 is of the form bx - ay + k = 0
(iii) If the two lines are parallel or coincident, then m1= m2
(iv) Any line parallel to ax + by + c = 0 is of the form ax + by + k = 0
(v) If any of the two lines is perpendicular to x-axis, then the slope of that line is infinite.
Let m1 = ∝ ,  or θ = |90° – a |, where tan a = m2
or θ = |90° – a |, where tan a = m2
i.e. angle θ is the complimentary to the angle which the oblique line makes with the x-axis.
(vi) If lines are equally inclined to the coordinate axis then m1 + m2 = 0
Ex.11 Find the equation to the straight line which is perpendicular bisector of the line segment AB, where A, B are (a,b) and (a', b') respectively.
Sol. Equation of AB is y - b = 
i.e. y (a' - a) - x (b' - b) = a'b - ab'.
Equation to the line perpendicular to AB is of the form (b' - b)y + (a' - a)x + k = 0 ....(1)
Since the midpoint of AB lies on (1), 
Hence the required equation of the straight line is 
(1) Equation of straight Lines passing through a given point and equally inclined to a given line :
Let the straight passing through the point (x1, y1) and make equal angles with the given straight line y = mx + c. If m is the slope of the required line and a is the angle which this line makes with the given line then 
(2) The above expression for tana, given two values of m, say mA and mB.
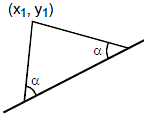
The required equations of the lines through the point (x1, y1) and making equal angles a with the given line are
y - y1 = mA(x - x1), y - y1 = mB (x - x1)
Ex.12 Find the equation to the sides of an isosceles right-angled triangled, the equation of whose hypotenuse is 3x + 4y = 4 and the opposite vertex is the point (2, 2).
Sol. The problem can be restarted as :
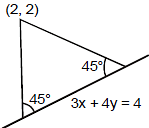
Find the equation to the straight lines passing through the given point (2, 2) and making equal angles of 45° with the given straight line 3x + 4y - 4 = 0. Slope of the line 3x + 4y - 4 = 0 is 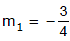
⇒  ,
,
i.e., 
mA =  , and mB = - 7
, and mB = - 7
Hence the required equations of the two lines are
y - 2 = mA(x - 2) and y - 2 = mB (x - 2) ⇒ 7y - x - 12 = 0 and 7x + y = 16.
|
75 videos|238 docs|91 tests
|
FAQs on Angle Between Two lines - Mathematics (Maths) Class 11 - Commerce
| 1. What is the formula to find the angle between two lines? |  |
| 2. How do I find the slope of a line given its equation? |  |
| 3. Can the angle between two lines be negative? |  |
| 4. How can I calculate the angle between two lines in degrees? |  |
| 5. What does it mean if the angle between two lines is 90 degrees? |  |

|
Explore Courses for Commerce exam
|

|

















