Angles and shape: Reflection & Translation | Year 5 Mathematics PDF Download
What is reflection?
- Reflection is a type of transformation that requires a mirror line.
- When a shape is reflected, its size remains the same; it only appears 'flipped'.
- Each point on the shape is equidistant from the mirror line on the opposite side.
- Using squared paper can be helpful for reflecting an object.
Examples
Example: 1
Let's take a look at another example:
The letters represent the coordinates of the original shapes vertices.
A - (3, 1)
B - (5, 1)
C - (4, 4)
D - (6, 4)
Like before, reflect each vertex of the shape in the mirror line.
Remember to make sure that each vertex is the same amount of squares away from the mirror line as the original shape. Now you have plotted the new vertices, join them to create the reflected shape.
Now you have plotted the new vertices, join them to create the reflected shape.
Can you see how the reflected vertices now have new coordinates?
Let’s see what they are:
Example: 2
Let's go through the steps to reflect a shape.
When reflecting a shape, you don't need to reflect the entire shape at once.
Instead, reflect each vertex (corner) of the shape, ensuring each vertex is the same distance from the mirror line as in the original shape. Once you have plotted the reflected vertices, connect the points together.
Once you have plotted the reflected vertices, connect the points together. This will give you the reflected shape.
This will give you the reflected shape.
When reflecting shapes on a grid, follow the same steps, and the reflected shape will have new coordinates.
What is translation?
Translation describes the movement of shapes up, down, left, and right.
Let's begin with a simple task: moving the furniture in Boo's bedroom using translation. Here is a floor plan showing the furniture in Boo's room.
Here is a floor plan showing the furniture in Boo's room.
Examples
Example: 1
Boo moves the bed to a new position. How many squares has she moved her bed by?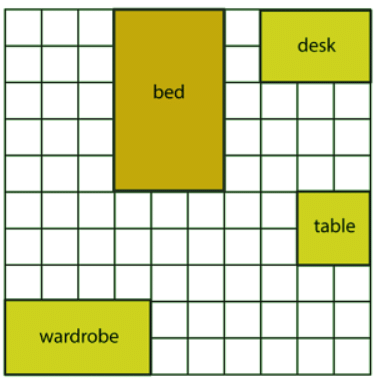
She has moved her bed by 3 squares.
When a shape is translated, each of the vertices (corners) must be moved in exactly the same way.
The bed has four corners which we've labelled vertex a, b, c and d.
If you count along the squares from each corner you'll see that each vertex has moved 3 squares to the right.
Example: 2
Boo has moved the table to a new position. The table has been moved diagonally, which means the shape has translated up or down as well as left or right.
The table has been moved diagonally, which means the shape has translated up or down as well as left or right.
If we translate one vertex at a time we can see that vertex a has translated 3 squares down and 3 squares to the left.
|
45 videos|42 docs|11 tests
|

|
Explore Courses for Year 5 exam
|

|
















