Angular momentum and torque | Basic Physics for IIT JAM PDF Download
A particle of mass m and velocity v has linear momentum p = mv. The particle may also have angular momentum L with respect to a given point in space. If r is the vector from the point to the particle, then
L = r × p (43)
Notice that angular momentum is always a vector perpendicular to the plane defined by the vectors r and p (or v). For example, if the particle (or a planet) is in a circular orbit, its angular momentum with respect to the centre of the circle is perpendicular to the plane of the orbit and in the direction given by the vector cross product right-hand rule, as shown in Figure 10. Moreover, since in the case of a circular orbit, r is perpendicular to p (or v), the magnitude of L is simply 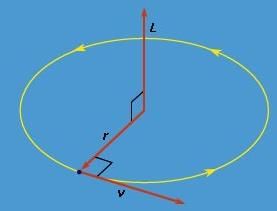
Figure: The angular momentum L of a particle traveling in a circular orbit.
L = rp = mvr (44)
The significance of angular momentum arises from its derivative with respect to time,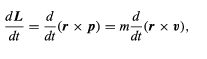 (45)
(45)
where p has been replaced by mv and the constant m has been factored out. Using the product rule of differential calculus,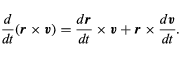 (46)
(46)
In the first term on the right-hand side of equation (46), dr/dt is simply the velocity v, leaving v × v. Since the cross product of any vector with itself is always zero, that term drops out, leaving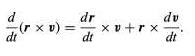 (46)
(46)
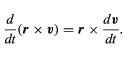 (47)
(47)
Here, dv/dt is the acceleration a of the particle. Thus, if equation (47) is multiplied by m, the left-hand side becomes dL/dt, as in equation (45), and the right-hand side may be written r × ma. Since, according to Newton’s second law, ma is equal to F, the net force acting on the particle, the result is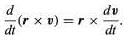 (47)
(47)
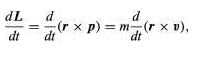 (45)
(45)
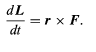 (48)
(48)
Equation (48) means that any change in the angular momentum of a particle must be produced by a force that is not acting along the same direction as r. One particularly important application is the solar system. Each planet is held in its orbit by its gravitational attraction to the Sun, a force that acts along the vector from the Sun to the planet. Thus, the force of gravity cannot change the angular momentum of any planet with respect to the Sun. Therefore, each planet has constant angular momentum with respect to the Sun. This conclusion is correct even though the real orbits of the planets are not circles but ellipses. (48)
(48)
The quantity r × F is called the torque τ. Torque may be thought of as a kind of twisting force, the kind needed to tighten a bolt or to set a body into rotation. Using this definition, equation may be rewritten
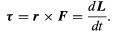 (49)
(49)
Equation (49) means that if there is no torque acting on a particle, its angular momentum is constant, or conserved. Suppose, however, that some agent applies a force Fa to the particle resulting in a torque equal to r× Fa. According to Newton’s third law, the particle must apply a force −Fa to the agent. Thus, there is a torque equal to −r × Fa acting on the agent. The torque on the particle causes its angular momentum to change at a rate given by dL/dt = r × Fa. However, the angular momentum La of the agent is changing at the rate dLa/dt = −r × Fa. Therefore, dL/dt + dLa/dt = 0, meaning that the total angular momentum of particle plus agent is constant, or conserved. This principle may be generalized to include all interactions between bodies of any kind, acting by way of forces of any kind. Total angular momentum is always conserved. The law of conservation of angular momentum is one of the most important principles in all of physics.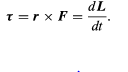 (49)
(49)
|
210 videos|156 docs|94 tests
|
FAQs on Angular momentum and torque - Basic Physics for IIT JAM
| 1. What is angular momentum in physics and how is it related to torque? |  |
| 2. How is angular momentum conserved in a closed system? |  |
| 3. Can angular momentum be negative? |  |
| 4. What are some real-life examples where angular momentum and torque are important? |  |
| 5. How does understanding angular momentum and torque help in engineering and design? |  |

|
Explore Courses for Physics exam
|

|

















