B Com Exam > B Com Notes > Business Mathematics and Statistics > Antiderivatives - Integration, Business Mathematics & Statistics
Antiderivatives - Integration, Business Mathematics & Statistics | Business Mathematics and Statistics - B Com PDF Download
Antiderivatives
An antiderivative of a function f is a function whose derivative is f . In other words, F is an antiderivative of f if F' = f . To find an antiderivative for a function f , we can often reverse the process of differentiation.
For example, if f = x4, then an antiderivative of f is 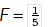 which can be found by reversing the power rule. Notice that not only is
which can be found by reversing the power rule. Notice that not only is 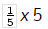 an antiderivative of f , but so are
an antiderivative of f , but so are 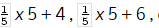 etc. In fact, adding or subtracting any constant would be acceptable.
etc. In fact, adding or subtracting any constant would be acceptable.
This should make sense algebraically, since the process of taking the derivative (i.e. going from F to f ) eliminates the constant term of F.
Because a single continuous function has infinitely many antiderivatives, we do not refer to "the antiderivative", but rather, a "family" of antiderivatives, each of which differs by a constant. So, if Fis an antiderivative of f , then G = F + c is also an antiderivative of f , and F and G are in the same family of antiderivatives.
Indefinite Integral
The notation used to refer to antiderivatives is the indefinite integral. f (x)dx means the antiderivative of f with respect to x . If F is an antiderivative of f , we can write
f (x)dx = F + c . In this context, c is called the constant of integration.
- x n dx =
x n+1 + c as long as n does not equal -1. This is essentially the power rule for derivatives in reverse
cf (x)dx = c
f (x)dx . That is, a scalar can be pulled out of the integral.
(f (x) + g(x))dx =
f (x)dx +
g(x)dx . The antiderivative of a sum is the sum of the antiderivatives.
sin(x)dx = - cos(x) + c
cos(x)dx = sin(x) + c
sec2(x)dx = tan(x) + c
These are the opposite of the trigonometric derivatives.
The document Antiderivatives - Integration, Business Mathematics & Statistics | Business Mathematics and Statistics - B Com is a part of the B Com Course Business Mathematics and Statistics.
All you need of B Com at this link: B Com
|
124 videos|176 docs
|
FAQs on Antiderivatives - Integration, Business Mathematics & Statistics - Business Mathematics and Statistics - B Com
| 1. What is an antiderivative in integration? |  |
Ans. An antiderivative is the reverse process of differentiation in calculus. It refers to finding a function whose derivative is equal to a given function. In other words, if F'(x) = f(x), then F(x) is called the antiderivative of f(x). Integration is the process of finding antiderivatives.
| 2. How is finding antiderivatives useful in business mathematics? |  |
Ans. Finding antiderivatives in business mathematics is essential for various applications. It helps in analyzing and solving problems related to optimization, revenue and cost functions, profit maximization, and marginal analysis. By determining antiderivatives, businesses can make informed decisions and improve their strategies.
| 3. What is the connection between antiderivatives and statistics in business? |  |
Ans. In business statistics, antiderivatives play a crucial role in probability distributions. Probability density functions (PDFs) are often defined as derivatives of cumulative distribution functions (CDFs). By integrating PDFs, businesses can determine probabilities of specific events or outcomes, which aids in statistical analysis and decision-making.
| 4. Can you provide an example of antiderivatives used in business mathematics? |  |
Ans. Certainly! One example is the calculation of total revenue. If the revenue function R(x) represents the income generated by selling x units of a product, finding the antiderivative of R'(x) gives us the total revenue function R(x). This helps businesses determine the overall income based on the quantity of products sold.
| 5. How can I improve my understanding and skills in finding antiderivatives for business applications? |  |
Ans. To improve your understanding and skills in finding antiderivatives for business applications, it is recommended to practice solving various integration problems. Familiarize yourself with different techniques such as the power rule, substitution, and integration by parts. Additionally, studying real-world business scenarios and their mathematical representations will enhance your ability to apply antiderivatives effectively.
Related Searches





















