Applications of Le Chatelier’s principle & Free Energy | Physical Chemistry PDF Download
12. Le-Chatelier’s Principle and Physical Equilibria
Le Chatelier’s principle, as already stated, is applicable to all types of equilibria involving not only chemical but physical changes as well. A few example of its application to physical equilibria are discussed below.
1. Vapour Pressure of a Liquid: Consider the equilibrium

It is well known that the change of a liquid into its vapour is accompanied by absorption of heat whereas the conversion of vapour into liquid state is accompanied by evolution of heat. According to Le Chatelier’s principle, therefore, addition of heat to such a system will shift the equilibrium towards the right. One raising the temperature of the system, liquid will evaporate. This will raise the vapour pressure of the system. Thus, the vapour pressure of a liquid increases with rise in temperature.
2. Effect of pressure on the boiling point of a liquid: The conversio n o f liquid into vapour, as represented by the above equilibrium, is accompanied by increase of pressure (vapour pressure). Therefore, if pressure on the system is increased, some of the vapour will change into liquid so as to lower the pressure. Thus, the application o f pressure on the system tends to condense the vapour into liquid state at a given temperature. In order to counteract it a higher temperature is needed. This explains the rise of boiling point of a liquid on the application of pressure.
Effect of pressure on the freeing point of a liquid (or melting point of a solid): At the melting point, solid and liquid are in equilibrium:
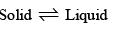
Now, when a solid melts, there is usually a change, either increase or decrease, of volume. For example, when ice melts, there is decrease in volume, or at constant volume, there is decrease in pressure. Thus, increase of pressure on ice  water system at a constant temperature will cause the equilibrium to shift towards the right, i.e., it will cause the ice to melt. Hence, in order to retain ice in equilibrium with water at the higher pressure it will be necessary to lower the temperature. Thus, the application o f pressure will lower the melting point of ice.
water system at a constant temperature will cause the equilibrium to shift towards the right, i.e., it will cause the ice to melt. Hence, in order to retain ice in equilibrium with water at the higher pressure it will be necessary to lower the temperature. Thus, the application o f pressure will lower the melting point of ice.
When sulphur melts there is increase in volume or at constant volume, there is increase in pressure. From similar considerations, it follows that if the pressure on the system, sulphur (solid)  sulphur (liquid) is increased, the melting point is raised.
sulphur (liquid) is increased, the melting point is raised.
Effect of temperature on solubility: In most cases, when a solute passes into solution, heat is absorbed, i.e., cooling results. Therefore according to Le Chatelier’s principle when heat is applied to a saturated heat (i.e., which tends to produce cooling). Therefore, some more of the solute will dissolve. In other words, the solubility of the substance increases with rise in temperature.
Dissociation of a few salts (e.g., calcium salts of organic acids) is accompanied by evolution of heat. In such cases evidently, the solubility decreases with rise in temperature.
13. Free Energy and Chemical Equilibrium
The Gibbs free energy function is true measure of chemical affinity under conditions of constant temperature and pressure. The free energy change in a chemical can be defined as
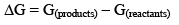
When ΔG = 0, there is no net work obtainable. The system is in a state of equilibrium. When ΔG is positive, net work must be put into the system to effect the reaction, otherwise it cannot take place. When ΔG is negative, the reaction can proceed spontaneously with accomplishment of the net work. The larger the amount of this work that can be accomplished, the farther away is the reaction from equilibrium. For this reason -ΔG has often been called the driving force of the reaction. From the statement of the reactants and products. It also depends upon the temperature and pressure which determine the molar free energies of the reactants and products.
The reaction conducted at constant temperature (i.e., in a thermostat)
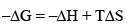
The driving force is made up of two parts, –ΔH term and TΔS term. -ΔH term is the heat of reaction at constant pressure and TΔS is heat involved when the process is carried out reversibly. The difference is the amount of heat of reaction which can be converted into net work (-ΔG), i.e., total heat minus unavailable heat.
If the reaction is carried out at constant volume, the decrease in Helmholtz function ΔG. ΔE + TΔS would be the proper measure of affinity of the reactant or the driving force of the reaction.
Now we can see why Berthollet and Thompson were wrong in assuming that driving force of the reaction was the heat of reaction. They neglected the TΔS term. The reasons for the apparent validity of their principle was that for many reactions, ΔH term far out weights the TΔS term. This is especially true at low temperature, since at higher temperature, TΔS term increases. The fact that driving force for a reaction is large (ΔG is large negative quantity) does not mean that the reaction will necessarily occur under any given conditions.
For example, the reaction
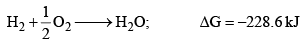
Does not occur at the laboratory temperature. The reaction mixture may be kept for years without any detectable formation of water. Here ΔH factor favours, but ΔS factor disfavours the reaction.
Similarly, the reaction

Is not favoured. However, the thermite reaction
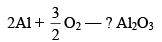
With large value of –ΔG proceeds favourably.
Standard Free Energy and Equilibrium Constant: The change in free energy for a reaction taking place between gaseous reactants and products represented by the general equation.
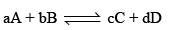
According to Van’t Hoff reaction isotherm
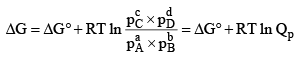
The condition for a system to be at equilibrium is that
ΔG = 0
Thus at equilibrium
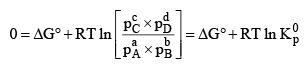
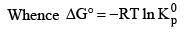
Note:
1. In the reaction, where all gaseous reactants and products; K represents Kp
2. In the reaction, where all solution reactants and products; K represents Kc
3. A mixture of solution and gaseous reactants; Kx represents the thermodynamic equilibrium constant and we do not make the distinction between Kp and Kc. We may conclude that for standard reactions, i.e., at 1 M or 1 atm.

|
84 videos|142 docs|67 tests
|
FAQs on Applications of Le Chatelier’s principle & Free Energy - Physical Chemistry
| 1. What is Le Chatelier's principle and how is it applied in chemical reactions? |  |
| 2. Can Le Chatelier's principle be used to explain the effect of temperature on an equilibrium reaction? |  |
| 3. How does Le Chatelier's principle explain the effect of pressure on a gaseous equilibrium reaction? |  |
| 4. What are the applications of Le Chatelier's principle in industry? |  |
| 5. How is Le Chatelier's principle related to the concept of free energy? |  |





















