Area of A Triangle using Determinants | Applied Mathematics for Class 12 - Commerce PDF Download
Determinant To Find Area of A Triangle
We know what a determinant is, let us know how to use Determinant to find Area of a Triangle
Suppose we are given three points in the Cartesian plane as (x1, y1), (x2, y2) and (x3, y3). The area of the triangle obtained by joining these points is given by,
Where α denotes the area of the triangle and (x1, y1), (x2, y2) and (x3, y3), represent the vertices of the triangle.
The formula for finding area could be represented in the form of determinants as given below.

The determinant represents the signed area of a triangle formed by three points. To ensure a positive area, we take the absolute value of the determinant. If the area is known, both positive and negative determinants are considered. If the points are collinear, forming a straight line, the determinant is zero, indicating zero area. To calculate the area using determinant expansion techniques, minors and cofactors are employed.
Therefore,

Hence, we see how determinants are applied to make calculations easy. Now let us try our hands at this application of determinants to find out the area of triangles.
Example1: Find out the area of the triangle whose vertices are given by A(0,0) , B (3,1) and C (2,4).
Sol: Using determinants we can easily find out the area of the triangle obtained by joining these points using the formula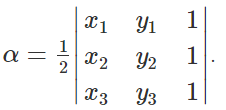
Substituting the respective values in the determinant we have
Expanding the above determinant by using expansion techniques of determinant we get,
α = 1/2 [0(1−4)–0(3−2)+1(12−2)]
⇒ α = 5units
Example2: Find the area of the triangle whose vertices are A ( 1, 1 ), B ( 4, 2 ), and C ( 3, 5)
Sol: Using the formula that we have previously learnt, we can find out the area of the triangle by joining the point given in the formula


When you substitute the given values in the above formula, we get:
k = ½ (1 ( 2 - 5 ) - 4 ( 4 - 3 ) + 3 ( 20 - 3 ))
k = ½ (1 ( -3 ) -4 ( 1 ) + 3 ( 17 ))
k = ½ (- 3 - 4 + 51)
k = ½ (44)
k = 22 units.
Since the area of the triangle cannot be negative, the value of k = 3 units.
|
58 videos|101 docs|63 tests
|
FAQs on Area of A Triangle using Determinants - Applied Mathematics for Class 12 - Commerce
| 1. How can I use the determinant to find the area of a triangle? |  |
| 2. Can I find the area of any triangle using the determinant method? |  |
| 3. What is the significance of dividing the determinant by 2 when finding the area of a triangle? |  |
| 4. Are there any other methods to find the area of a triangle besides using the determinant? |  |
| 5. Can the determinant method be extended to find the area of triangles in three-dimensional space? |  |

|
Explore Courses for Commerce exam
|

|

















