Arithmetic Progression (A.P) | Mathematics (Maths) Class 11 - Commerce PDF Download
Sequence and Series
A. Sequence
A sequence is a set of terms in a definite order with a rule for obtaining the terms.
e.g. 1 , 1/2 , 1/3 , ....... , 1/n , ........ is a sequence .
A sequence is a function whose domain is the set N of natural numbers. Since the domain for every sequence is the set of N natural numbers, therefore a sequence is represented by its range. f : N → R, then f(n) = tn n ε N is called a sequence and is denoted by
{f(1), f(2), f(3),................} =
{t1, t2, t3,.........................} = {tn}
Real Sequence : A sequence whose range is a subset of R is called a real sequence.
Examples :
(i) 2, 5, 8, 11, ...........
(ii) 4, 1, -2, -5, ............
(iii) 3, -9, 27, -81, ...........
Types of Sequence : On the basis of the number of terms there are two types of sequence.
(i) Finite sequence : A sequence is said to be finite if it has finite number of terms.
(ii) Infinite sequence : A sequence is said to be infinite if it has infinite number of terms.
Series : By adding or substracting the terms of a sequence, we get an expression which is called a series. If a1, a2, a3, ......., an is a sequence, then the expression a1 + a2 + a3+ ...... + an is a series.
Example.
(i) 1 + 2 + 3 + 4 + ............ + n
(ii) 2 + 4 + 8 + 16 + ..............
Progression : It is not necessary that the terms of a sequence always follow a certain pattern or they are described by some explicit formula of the nth term. Those sequences whose terms follow certain patterns are called progressions.
Ex.1 Write down the sequence whose nth term is
(i) (-1)n
(ii) 
Sol. (i) Let an = (-1)n . Putting = 1, 2, 3, 4,...... successively, we get
. Putting = 1, 2, 3, 4,...... successively, we get
a1 = (-1)1 = - 1
= - 1
a2 = (-1)2 = 8/5
= 8/5
a3 = (-1)3 = -11/5
= -11/5
a4 = (-1)4 = 14/5
= 14/5
..........................................
Hence we obtain the sequence -1, 8/5, -11/5, 14/5,......
(ii) Let an =  . Putting n = 1, 2, 3, 4,... successively, we get
. Putting n = 1, 2, 3, 4,... successively, we get
a1 = 
a2 = 
a3 =  = 0
= 0
a4 = 
...........................................
Hence we obtain the sequence  /2,
/2,  /8, 0, -
/8, 0, - /32,...
/32,...
Ex.2 If sum of n terms of a sequence is given by Sn = 2n2 + 3n, find its 50th term.
Sol. Let tn is nth term of the sequence so tn = sn - sn - 1 = 2n2 + 3n - 2(n - 1)2 - 3 (n - 1) = 4n + 1
so t50 = 201.
B. Arithmetic Progression (AP)
AP is a sequence whose terms increase or decrease by a fixed number . This fixed number is called the common difference . If a is the first term & d the common difference, then AP can be written as a , a + d , a + 2 d , ....... a + (n - 1) d , ....... .
nth term of this AP
tn = a + (n - 1) d, where d = an - an-1 .
The sum of the first n terms of the AP is given by ; Sn =  [2 a + (n - 1)d] =
[2 a + (n - 1)d] =  [a + l] .
[a + l] .
where l is the last term.
Remarks :
(i) If each term of an A.P. is increased, decreased, multiplied or divided by the same non zero number, then the resulting sequence is also an AP .
(ii) Three numbers in AP can be taken as a - d , a , a + d ; four numbers in AP can be taken as a - 3d, a - d, a + d, a + 3d ; five numbers in AP are a - 2d , a - d , a, a + d, a + 2d & six terms in AP are a - 5d, a - 3d, a - d, a + d, a + 3d, a + 5d etc.
(iii) The common difference can be zero, positive or negative .
(iv) The sum of the terms of an AP equidistant from the beginning & end is constant and equal to the sum of first & last terms .
(v) Any term of an AP (except the first) is equal to half the sum of terms which are equidistant from it .
an = 1/2 (an-k + an+k), k < n .
For k = 1, an = (1/2) (an-1+ an+1) ; For k = 2, an = (1/2) (an-2+ an+2) and so on .
(vi) tr = Sr - Sr-1
(vii) If a , b , c are in AP ⇒ 2 b = a + c.
Ex. 3 Find the sum of all the three digit natural numbers which on division by 7 leaves remainder 3.
Sol. All these numbers are 101, 108, 115,....... 997, to find n.
997 = 101 + (n - 1) 7 ⇒ n = 129
so S = [101 + 997] = 70821.
Ex. 4 The sum of first three terms of an A.P. is 27 and the sum of their squares is 293 . Find the sum to 'n' terms of the A.P.
Sol. Let a - d , a , a + d be the numbers ⇒ a = 9
Also (a - d)2 + a2 + (a + d)2 = 293. ⇒ 3a2 + 2d2 = 293 ⇒ d2 = 25 ⇒ d = ± 5
therefore numbers are 4, 9, 14.
Hence the A.P. is 4, 9, 14, ......
⇒ sn =  [5 n + 3] or 14, 9, 4, .....
[5 n + 3] or 14, 9, 4, .....
⇒ sn =  [33 - 5 n]
[33 - 5 n]
Ex.5 Let an be the nth term of an arithmetic progression. Let Sn be the sum of the first n terms of the arithmetic progression with a1 = 1 and a3 = 3a8. Find the largest possible value of Sn.
Sol. From a3 = 3a8 we obtain 1 + 2d = 3(1 + 7d) ⇒ d = - 2/19.
Then Sn =  =
=  [19 - (n - 1)] =
[19 - (n - 1)] =  .
.
now consider 20n - n2 = - [n2 - 20n] = - [(n - 10)2 - 100]
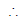 Sn =
Sn =  now, Sn will be maximum if n = 10 and (Sn)max =
now, Sn will be maximum if n = 10 and (Sn)max = 
Ex.6 Suppose a1, a2,.... are in A.P. and Sk denotes the sum of the first k terms of this A.P. If Sn/Sm = n4/m4 for all m, n, ε N, then prove that 
Sol. Putting a1 = a, we have

Replacing n by 2n + 1 and m by 2m + 1, we get

⇒ 
Ex.7 If the sum of m terms of an A.P. is equal to the sum of either the next n terms or the next p terms prove that (m + n)  = (m +p)
= (m +p) 
Sol. Let the A.P. be a, a + d, a + 2d,....
Given T1 + T2 + ... + Tm = Tm + 1 + Tm + 2 +....+Tm + n ...(1)
Adding T1 + T2 + .... + Tm on both sides in (i), Then
2(T1 + T2+....+Tm) = T1 + T2 + ....+ Tm + Tm + 1 +... +....+Tm + n ⇒ 2 Sm = Sm + n
∴ 2.  {2a + (m - 1)d} =
{2a + (m - 1)d} =  {2a + (m + n - 1) d}
{2a + (m + n - 1) d}
Let 2a + (m - 1)d = x
⇒ mx =  {x + nd} ...(2)
{x + nd} ...(2)
⇒ (m - n) x = (m + n) nd
again T1 + T2 + .... + Tm = Tm + 1 + Tm + 2 +....+Tm + p ...(3)
Similarly (m - p) x = (m + p) pd
dividing (2) by (3), we get 
⇒(m - n) (m + p) p = (m - p) (m + n) n
dividing both sides by mnp, we have (m + p)  = (m + n)
= (m + n) 
Hence (m + n)  = (m + p)
= (m + p) 
Ex.8 Show that any positive integral power (except the first) of a positive integer m, is the sum of m consecutive odd positive integers. Find the first odd integer for mr (r > 1).
Sol. Let us find k such that mr = (2k + 1) + (2k + 3) + .... + (2k + 2m - 1)
∴ mr =  [2k + 1 + 2k + 2m - 1]
[2k + 1 + 2k + 2m - 1]
⇒mr - 1 = 2k + m
Note that mr - 1 - m is an even integer for all r, m ε N and r > 1. Therefore, k = (mr - 1 - m)/2 is an integer. Thus, the first term is given by mr - 1-m + 1.
|
75 videos|238 docs|91 tests
|
FAQs on Arithmetic Progression (A.P) - Mathematics (Maths) Class 11 - Commerce
| 1. What is an arithmetic progression? |  |
| 2. How can I find the common difference in an arithmetic progression? |  |
| 3. How do I find the nth term of an arithmetic progression? |  |
| 4. Can an arithmetic progression have negative terms? |  |
| 5. How can I determine the sum of an arithmetic progression? |  |

|
Explore Courses for Commerce exam
|

|


















