Assignment - Polynomials, Class 9 Mathematics PDF Download
TRUE AND FALSE TYPE QUESTIONS
1. When 14x3 – 3x2 + 4x + 2 is divided by 2x – 1, the remainder is 5.
2. 4x2 – 8x + 15 is exactly divisible by 2x – 1.
3. x2 – 5x + 6 cannot be written as a product of two linear factors.
4. x3 – 3x2y + 3xy2 – y3 is exactly divisible by x – y.
5. (2a + b)2 – (2b + a)2 = 3(a2 – b2) is an identify.
6. (x2 + 1)4 = (x4 – 6x2 + 1)2 + 16 (x3 – x)2 in an identity.
FILL IN THE BLANKS
1. If a + b = 2, then the value of a3 + b3 + 6ab is equal to .......................
2. The coefficient of 'a' in (a + b + c) (x + y + z) + (b + c – a) (x + y – z) + (c + a – b) (y + z – x) is .......................
3. (x + y)2 + (x – y)2 ÷ 
reduces to .......................
4. The expression 
for all values of x. Then A and B are respectively equal to............
5. The coefficient of x2 in (px2 + 4x + r) × (4x2 – 3qx – 5) is .......................
6. The value of {x + (y – z)}2 – {y – (z + x)}2 + {z – (x + y)}2 when x = 1, y = –2, z = 3 is equal to .......................
7. 
then the value of m .......................
8. abx2 + (a2 – b2)x – ab when expressed in linear factors is equal to .......................
9. x2 (y – z) + y2(z – x) + z2(x – y) = N(x – y) (y – z), (z – x), then N must have value .......................
10. 4x2 – 2bx + ab – a2 when expressed in linear factors is equal to .......................
VERY SHORT ANSWER TYPE QUESTIONS
1. Which of the following expressions are polynomial or not :
(i) 11x + 1
(ii) 7x2 – 5x + 5
(iii) t3 – 2t + 1
2. Write the coefficient of x3 in each of the following :
(i) 3x3 – 3x + 2 (ii) 14x3 – 2x3 + 5x – 7x2 (iii) √2 x2 + 1 (iv) 3/4x3 + 2x – 3
3. Write the degree of each of the following polynomials :
(i) 3x2 – 4x + 2 (ii) 7x3 + 2x2 + x (iii) 5 – x2 (iv) 1 + 2x + 3x2 – 11x4
4. Classify the following as linear, quadratic and cubic polynomials :
(i) x3 – 4 (ii) x2 + 1 (iii) 5x2 – 3x + 7 (iv) 1 + 5x (v) 4r3
5. Find the value of the following polynomial at the indicate value of variables :
(i) p(x) = 5x2 – 3x + 7 at x = 1
(ii) q(y) = 3y2 – 4y + √2 at y = 2
(iii) p(t) = 4t4 + 5t3 – t2 + 6 at t = a
6. Find the zeroes of each of the following polynomials :
(i) P(x) = x – 4
(ii) g(x) = 2x + 1
(iii) P(x) = (x + 1) (x + 2)
(iv) P(x) = (x –1) (x – 2) (x – 3)
(v) P(x) = 7x2
(vi) P(x) = rx + s, r 
0
7. Verify whether the following are zeroes of the polynomial indicated against them :
(i) P(x) = 5x – 1, x = 15
(ii) P(x) (x – 2) (x – 5), x = 2, 5
(iii) S(x) = x2, x = 0, 1
(iv) P(x) = 3x2 – 1, 
(v) g(x) = 5x2 + 7x, x = 0, –7/5
8. Use remainder theorem to find remainder when P(x) is dividedby q(x) in the following questions :
(i) P(x) = 2x2 – 5x + 7, q(x) = x – 1
(ii) P(x) = x9 – 5x4 + 1, q(x) = x + 1
(iii) P(x) = 4x3 – 12x2 + 11x – 5, q(x) = x – 1
2
(iv) P(x) = x4 + x3 + x2 – 5x + 1 q(x) = x + 1
Use factor theorem to verify in each of the following that q(x) is a factor of p(x)
9. (i) P(x) = 3x2 – 5x + 2, q(x) = 3x – 2
(ii) P(x) = x4 – x3 + x – 1 q(x) = x + 1
(iii) P(x) = x5 – x4 + 3x2 – 2x + 4 q(x) = x – 2
10. Find the value of k if (x – 2) is a factor of 2x3 – 6x2 + 5x + k.
11. Find the value of k if (x + 3) is a factor of 3x2 + kx + 6.
12. For what value of k is y3 + ky + 2k – 2 exactly divisible by (y + 1) ?
13. For what value of m is 2x3 + mx2 + 11x + m + 3 exactly divisible by (2x – 1) ?
14. Find the value of a if (2y + 3) is a factor of 2y3 + 9y2 – y – a.
15. Show that 3 is a zero of the polynomial x3 + x2 – 17x + 15.
16. Show that –1 is a zero of the polynomial 2x3 – x2 + x + 4.
17. Show that 1 is not a zero of the polynomial 4x4 – 3x3 + 2x2 – 5x + 1.
18. Using factor theorem, show that a – b is a factor of a(b2 – c2) + b(c2 – a2) + c(a2 – b2).
19. Using factor theorem, factorize the polynomial x2 – 5x + 6.
20. Find the value of p, if (x + 1) is a factor of polynomial 2x3 – 2x2 + x + p.
21. Find the value of a, if x + 2 is a factor of x3 – 2ax2 + 16.
FACTORIZE EACH OF THE FOLLOWING EXPRESSIONS
22. x2 – x – 42.
23. 1 + 2x + x2.
24. 6 – 5y – y2.
25. x2 – 9ax + 18a2.
26. a2 + 46a + 205.
27. k2 – 26k + 133.
28. ab + ac – b2 – bc.
29. 2xy – x + z – 2zy.
30. 100 – 9p2.
31. p4 – 81q4.
32. 1/5x2 + 2x – 15.
33. 7√2 x2 – 10x – 4√2 .
34. 6xy + 6 – 9y – 4x.
35. 1 – 256x4.
36. x4 – (2y – 3z)2.
37. (2a + 1)2 – 9b4.
38. 24√3 x3 – 125y3.
39. 
40. a6x4 – a4x6.
41. If one of the factors of x2 + x – 20 is (x + 5), find other factor.
42. Find the positive squares root of 36x2 + 60x + 25.
43. Simplify : (i)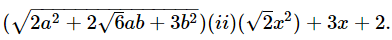 
44. Factorise : 5(a + 2b)2 – 7(a + 2b) + 2.
45. Factorise : 125(x – y)3 + (5y – 3z)3 + (3z – 5x)3.
46. Factorise : 27x3 + y3 + z3 – 9xyz.
47. Find the product : (i) (x + 2) (x + 9) (ii) (x + 8) (x – 2) (iii) (z – 3) (z – 5) (iv) (z2 + 4) (z2 – 5)
48. Evaluate the following : (i) 103 × 105 (ii) 98 × 99 (iii) 104 × 95
49. Write : 
in expand form.
50. Write : 
is expand form.
SHORT ANSWER TYPE QUESTION
51. Write the expansions of each of the following : (i) (9x + 2y + z)2 (ii) (3x – 2y – z)2
52. Simplify : (2a + b + c)2 + (2a – b – c)2
53. Write the expansion of the following : (i) (2x + 3y)3 (ii) (p – yz)3.
54. Find the value of 27x3 + 8y3 if 3x + 2y = 20 and xy = 14/9 .
55. Find the value of a3 – 27b3 if a – 3b = – 6 and ab = – 10.
56. Evaluate : (i) (101)3 (ii) (399)3.
57. Find the product of following :
(i) (x + 3) (x2 – 3x + 9) (ii) (5a – 3b) (25a2 + 15ab + 9b2)
58. Factorize :
(i) 1 – 27z3 (ii) 250x3 – 16y3 (iii) xy3 + 729x4
59. If x + y + z = 8 and xy + yz + zx = 20, find the value of x3 + y3 + z3 – 3xyz.
60. If a + b + c = 9 and a2 + b2 + c2 = 35, find the value of a3 + b3 + c3 – 3abc.
61. If p + q + r = 1 and pq + qr + pr = –1 and pqr = –1, find the value of p3 + q3 + r3.
62. Factorize : (x – y)3 + (y – z)3 + (z – x)3.
63. Find the value of : (25)3 – (29)3 + (4)3.
LONG ANSWER TYPE QUESTION
64. With out actual division, prove that a4 + 2a3 – 2a2 + 2a – 3 is exactly divisible a2 + 2a – 3.
65. If (x + 1) and (x – 1) are the factors of mx3 + x2 – 2x + n, find the value of m and n.
66. The polynomials kx3 + 3x2 – 3 and 2x3 – 5x + k when divided by (x – 4) leave the same remainder or in each case. Find the value of k.
67. What must be added to x3 – 3x2 – 12x + 19 so that result is exactly divisible by x2 + x – 6?
68. What must be subtrated from x3 – 6x2 – 15x + 80 so that result is exactly divisible by x2 + x – 12 ?
69. Using factor theorem, factorise the polynomial x4 – 2x3 – 7x2 + 8x + 12.
70. Let A and B are the remainders when the polynomial y3 + 2y2 – 5ay – 7 and y3 + ay2 – 12y + 6 are divided by y + 1 and y – 2 respectively. If 2A + B = 6, find the value of a.
71. Simplify : (a + b)3 + (a – b)3 + 6a(a2 – b2).
72. Show that if a + b is not zero, then the equation a(x – a) = 2ab – b(x – b) has a solution x = a + b.
73. Show that if 2(a2 + b2) = (a + b)2, then a = b.
74. Find the value of :
(i) x3 + y3 – 12xy + 64 when x + y = – 4
(ii) x3 – 8y3 – 36xy – 216 when x = 2y + 6.
(iii) (x – a)3 + (x – b)3 + (x – c)3 – 3(x – a) (x – b) (x – c) when a + b + c = 3x.
75. Prove that a3 + b3 + c3 – 3abc = 1
2 (a + b + c) [(a – b)2 + (b – c)2 + (c – a)2]
76. Prove that (a + b)3 + (b + c)3 + (c + a)3 – 3(a + b) (b + c) (c + a) = 2(a3 + b3 + c3 – 3abc)
77. If x2 – 1 is a factor of ax4 + bx3 + cx2 + dx + e, show that a + c + e = b + d = 0.
78. Using factor theorem, show that (x + y), (y + z) and (z + x) are the factors of (x + y – z)3 – (x3 + y3 + z3).
79. If (3x – 1)4 = a4x4 + a3x3 + a2x2 + a1x + a0, then find the value of a4 +3a3 + 9a2 + 27a1 + 81a0.
ANSWER KEY
TRUE & FALSE
1. T
2. F
3. F
4. T
5. T
6. T
FILL IN THE BLANKS
1. [8]
2. [–x + y + 3z]
3. 2xy
4. A = 2, B = –1
5. –5p – 12q + 4r
6. –4
7. 25
8. (bx + a) (ax – b)
9. –1
10. (2x – a) (2x – b + a)
VERY SHORT ANSWER TYPE QUESTIONS
1. (i), (ii), (iii), (vi)
2. (i) 1, (ii) –2, (iii) 0, (iv) 34
3. (i) 2, (ii) 3, (iii), 2, (iv) 4
4. (i) Cubic, (ii) Quadratic, (iii) Quadratic, (iv) Linear (v) Cubic
5. (i) 9, (ii) 4+ 11, (iii) 4a4 + 5a3 – a2 + 6
6. (i) 4, (ii) –1/2, (iii) –1, –2, (iv) 1, 2, 3, (v) 0, (vi) –s/r
7. (i) Yes, (ii) Yes, both, (iii) x = 0, x = 1 is not zero, (iv) 
is not zero (v) Yes, both
8. (i) 4, (ii) –5, (iii) –2, (iv) 7
10. [–2]
11. [11]
12. [3]
13. [–7]
14. [15]
19. (x – 2) (x – 3)
20. [p = 5]
21. [a = 1]
22. [(x + 6) (x – 7)]
23. [(x + 1)2]
24. (y – 1) (y + 6)
25. (x – 6a) (x – 3a)
26. (a + 41) (a + 5)
27. (k – 7) (k – 19)
28. (a – b) (b + c)
29. (x – z) (2y – 1)
30. (10 – 3p) (10 + 3p)
31. (p + 3q) (p – 3q) (p2 + 9q2)
32. 1/5(x + 15) (x – 5)
33. (x – √2 ) (7√2 x + 4)
34. (3y – 2) (2x – 3)
35. (1 – 4x) (1 + 4x) (1 + 16x2)
36. (x2 – 2y + 3z) (x2 + 2y – 3z)
37. (2a + 1 – 3b2) (2a + 1 + 3b2)
38. (2√3 x – 5y) (12x2 + 10√3 xy + 25y2)
39. (5a + b/3 ) (25a2 – 5/3 ab + b2/9 )
40. a4x4 (a – x) (a + x)
41. (x – 4)
42. (6x + 5)
43. (i) ( 2a + 3b), (ii) ( 2x + 1) (x + 2)
44. (5a + 10b – 2) (a + 2b – 1)
45. 3(5x – 5y) + (5y – 3z) + (3z – 5x)
46. (3x + y + z) (9x2 + y2 + z2 – 3xy – yz – 3xz)
47. (i) x2 + 11x + 18, (ii) x2 + 6x – 16, (iii) z – 8z + 5, (iv) z4 – z2 – 20
48. (i) 10815, (ii) 9702, (iii) 9880
49. 
50. 
SHORT ANSWER TYPE QUESTIONS
51. (i) 81x2 + 4y2 + z2 + 36xy + 4yz + 18zx, (ii) 9x2 + 4y2 + z2 – 12xy + 4yz – 6xz
52. [8a2 + 2b2 + 2c2 + 4bc]
53. (i) 8x3 + 27y3 + 36x.y + 54xy., (ii) p3 – y3z3 – 3p2yz + 3py2z2
54. [7440]
55. [324]
56. (i) 1030301, (ii) 63521199
57. (i) x3 + 27, (ii) [125a3 – 27b3]
58. (i) (1 – 3z) (1 + 3z + 9z2), (ii) 2(5x – 2y) (25x2 + 10xy + 4y2), (iii) x(y + 9x) (y2 + 81x – 9xy)
59. [32]
60. [108]
61. [1]
62. [3(x – y) (y – z) (z – x)]
63. [–8700]
LONG ANSWER TYPE QUESTIONS
65. [m = 2, n = –1]
66. [k = 1]
67. [2x + 5]
68. [4x – 4]
69. (x + 1) (x + 2) (x – 2) (x – 3)
70. [a = 2]
71. 8a3
74. (i) 0 (ii) 0 (iii) 0
79. [0]
FAQs on Assignment - Polynomials, Class 9 Mathematics
| 1. What are polynomials? |  |
| 2. What is the degree of a polynomial? | |
| 3. How do you add and subtract polynomials? | |
| 4. What is the factor theorem? | |
| 5. How do you solve polynomial equations? | |
|
29.8K Views |
|
4.95/5 Rating |
|
Dec 21, 2024 Last updated |
|
Explore Courses for Class 9 exam
|
|
past year papers
,Assignment - Polynomials
,Summary
,video lectures
,Viva Questions
,Class 9 Mathematics
,Semester Notes
,Extra Questions
,Important questions
,Objective type Questions
,Assignment - Polynomials
,Previous Year Questions with Solutions
,Assignment - Polynomials
,shortcuts and tricks
,mock tests for examination
,Class 9 Mathematics
,Class 9 Mathematics
,MCQs
,ppt
,Exam
,study material
,Free
,Sample Paper
,practice quizzes
;
Assignment - Polynomials, Class 9 Mathematics Free PDF Download
Importance of Assignment - Polynomials, Class 9 Mathematics
Assignment - Polynomials, Class 9 Mathematics Notes
Assignment - Polynomials, Class 9 Mathematics Class 9 Questions
Study Assignment - Polynomials, Class 9 Mathematics on the App
|
© EduRev
|
Education Revolution
|
|
