Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Averages from Tables
Averages from Tables | Mathematics for GCSE/IGCSE - Class 10 PDF Download
Averages from Tables & Charts
How do we find averages if there are lots of values?
- In practical scenarios, the volume of data available for analysis is typically extensive, extending beyond a few isolated figures.
- To facilitate comprehension, this data is commonly structured in formats like tables or charts, enhancing readability and interpretation.
- When presented in a tabular or graphical form, it remains possible to calculate statistical measures such as the mean, median, and mode.
- However, a crucial aspect involves grasping the underlying message conveyed by the table or chart.
How do I find averages from a table or chart?
- Finding the median and mode from tables/charts is quite simple once you grasp the information presented in the table or chart.
- Tables are essential for summarizing data neatly and, importantly, they arrange the data in order.
Finding the mean from (discrete) data presented in tables:
- Finding the mean from discrete data presented in tables involves understanding the information conveyed by the table.
- Tables provide the data value (e.g., the number of pets per household) and the frequency of that data value (e.g., the number of households with that number of pets).
- The mean can be determined once you understand the information in the table. Tables provide data values and their frequencies.
Steps to Calculate Mean from Table Data:
- Step 1: Add a column to the table to calculate 'data value' multiplied by 'frequency'. This step involves the preliminary computation required for determining the mean.
- Step 2: Calculate the total of the additional column to get the sum of all data values in the table.
- Step 3: Find the mean by dividing the total data value by the sum of frequencies, essentially dividing the overall data values by the count of data points.
Finding the median from (discrete) data presented in tables:
- Examine the data table to pinpoint the median's position accurately.
- The position of the median can be found by using
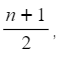 where n is the number of data values
where n is the number of data values - Use the table to deduce where the
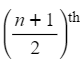 value lies
value lies- For instance, if the median corresponds to the 7th value and the cumulative frequencies of the preceding rows are 4 and 7, the median will be within the 7 values of the subsequent row.
Finding the mode (or modal value)
Identifying the mode (or modal value) is a straightforward process.
- Look for the value with the highest frequency in the data set.
- This high frequency corresponds to a specific data value.
- Ensure not to mistake the data value for the frequency itself.
- In a table, the frequency guides us to the row containing the mode.
Averages from Grouped Data
What is grouped data and why use it?
- When dealing with certain scenarios, data can exhibit significant variation. For instance, consider the heights of individuals, especially when the dataset comprises both children and adults.
- Data like height is considered continuous, meaning it can be measured. However, listing every single height value, especially in a mixed dataset, can be cumbersome.
- Due to minimal differences between adjacent values (e.g., someone being 176 cm tall versus 177 cm tall), it is common practice to group such data into classes.
- Grouping data into classes is a practical approach, but it comes with a trade-off: the loss of raw data. For example, knowing that 10 individuals have heights between 150 cm and 160 cm does not reveal the exact heights of those 10 people.
- Consequently, when data is grouped, the original raw data is obscured. This makes it challenging to calculate the precise mean, median, and mode using their traditional definitions. However, estimations can be made, especially when the term "estimate" is mentioned in questions.
- We can estimate the mean and identify the class interval within which the median falls.
- Similarly, we can determine the modal class, which denotes the class interval containing the mode.
How do I find/estimate the mean from grouped data?
- There is one extra stage to this method compared to finding the mean from tables with discrete data.
- We use the class midpoints as our data values. For example, if heights are split into class intervals 150 ≤ x < 160, 160 ≤ x < 170, etc., the midpoints, and so data values, would be 155, 165, etc.
- Step 1:
- Draw an extra two columns on the end of a table of the grouped data.
- In the first new column, write down the midpoint of each class interval.
- Step 2:
- Work out "frequency" × "midpoint" (This is often called fx).
- Step 3:
- Total the fx column, and if not already done nor mentioned in the question, total the frequency column to find the number of data values involved.
- Step 4:
- Estimate the mean by using its formula: "total of fx" ÷ "no. of data values".
- Step 1:
- Be careful with midpoints
- Not all class intervals will be of equal size, so there may not be a nice pattern to the midpoints.
How do I find the class interval that the median lies in?
- Find the median position by calculating n/2, where 𝑛n is the total number of data values (sum of the frequency column).
- Use the frequency table to locate the class interval that contains the (n/2)th value.
- For example, if the median position is the 7th value and the frequencies of the first two class intervals are 4 and 7 respectively, the median lies in the second class interval.
- When discussing the median in the context of grouped data, refer to the "class interval containing the median" rather than simply "the median."
How do I find the modal class interval?
- Focus on the class interval that contains the modal value, which is the class interval with the highest frequency.
- Locate the highest frequency in the table.
- Identify the class interval associated with this highest frequency.
- Ensure not to confuse the class interval with the frequency itself; the frequency indicates which class interval contains the mode.
Question for Averages from TablesTry yourself: How can the mean be calculated from discrete data presented in a table?View Solution
The document Averages from Tables | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
66 videos|674 docs|19 tests
|
FAQs on Averages from Tables - Mathematics for GCSE/IGCSE - Class 10
| 1. What is the most common method used to calculate averages from tables and charts? |  |
Ans. The most common method used to calculate averages from tables and charts is to sum up all the values and then divide by the total number of values.
| 2. How can grouped data be used to calculate averages effectively? |  |
Ans. Grouped data can be used to calculate averages effectively by finding the midpoint of each group, multiplying it by the frequency, summing up the results, and then dividing by the total frequency.
| 3. How can averages from tables and charts help in making informed decisions? |  |
Ans. Averages from tables and charts can help in making informed decisions by providing a summary of the data, highlighting trends or patterns, and enabling comparisons between different categories or time periods.
| 4. What are some common mistakes to avoid when calculating averages from tables and charts? |  |
Ans. Some common mistakes to avoid when calculating averages from tables and charts include not considering all the values, mistaking frequencies for actual values, and not following the correct formula for grouped data.
| 5. How can averages from tables and charts be used to identify outliers or anomalies in the data? |  |
Ans. Averages from tables and charts can be used to identify outliers or anomalies in the data by comparing individual values to the average and looking for values that deviate significantly from the norm.
Related Searches















