B + Tree | Database Management System (DBMS) - Computer Science Engineering (CSE) PDF Download
Introduction of B+ Tree
In order, to implement dynamic multilevel indexing, B-tree and B+ tree are generally employed. The drawback of B-tree used for indexing, however is that it stores the data pointer (a pointer to the disk file block containing the key value), corresponding to a particular key value, along with that key value in the node of a B-tree. This technique, greatly reduces the number of entries that can be packed into a node of a B-tree, thereby contributing to the increase in the number of levels in the B-tree, hence increasing the search time of a record.
B+ tree eliminates the above drawback by storing data pointers only at the leaf nodes of the tree. Thus, the structure of leaf nodes of a B+ tree is quite different from the structure of internal nodes of the B tree. It may be noted here that, since data pointers are present only at the leaf nodes, the leaf nodes must necessarily store all the key values along with their corresponding data pointers to the disk file block, in order to access them. Moreover, the leaf nodes are linked to provide ordered access to the records. The leaf nodes, therefore form the first level of index, with the internal nodes forming the other levels of a multilevel index. Some of the key values of the leaf nodes also appear in the internal nodes, to simply act as a medium to control the searching of a record.
From the above discussion it is apparent that a B+ tree, unlike a B-tree has two orders, ‘a’ and ‘b’, one for the internal nodes and the other for the external (or leaf) nodes.
The structure of the internal nodes of a B+ tree of order ‘a’ is as follows:
- Each internal node is of the form:
<P1, K1, P2, K2, ….., Pc - 1, Kc - 1, Pc>
where c <= a and each Pi is a tree pointer (i.e points to another node of the tree) and, each Ki is a key value (see diagram-I for reference). - Every internal node has: K1 < K2 < …. < Kc - 1
- For each search field values ‘X’ in the sub-tree pointed at by Pi, the following condition holds:
Ki-1 < X <= Ki, for 1 < i < c and, Ki - 1 < X, for i = c
(See diagram I for reference) - Each internal nodes has at most ‘a’ tree pointers.
- The root node has, at least two tree pointers, while the other internal nodes have at least \ceil(a/2) tree pointers each.
- If any internal node has ‘c’ pointers, c <= a, then it has 'c – 1' key values.
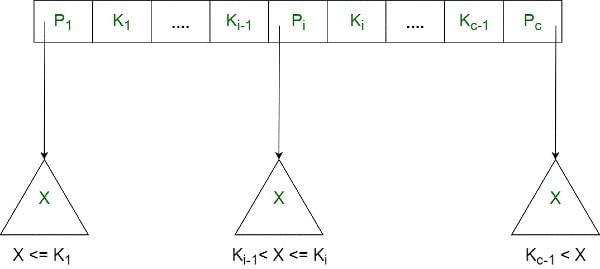 Diagram-I
Diagram-I
The structure of the leaf nodes of a B+ tree of order ‘b’ is as follows:
- Each leaf node is of the form :
<<K1, D1>, <K2, D2>, ….., <Kc - 1, Dc - 1>, Pnext>
where c <= b and each Di is a data pointer (i.e points to actual record in the disk whose key value is Ki or to a disk file block containing that record) and, each Ki is a key value and, Pnext points to next leaf node in the B+ tree (see diagram II for reference). - Every leaf node has : K1< K2 < …. < Kc - 1, c <= b
- Each leaf node has at least \ceil(b/2) values.
- All leaf nodes are at same level.
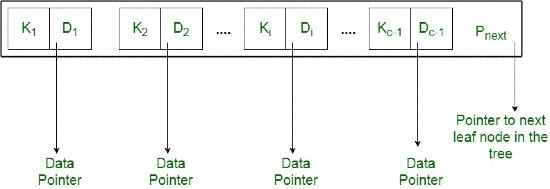 Diagram-II
Diagram-II
Using the Pnext pointer it is viable to traverse all the leaf nodes, just like a linked list, thereby achieving ordered access to the records stored in the disk.
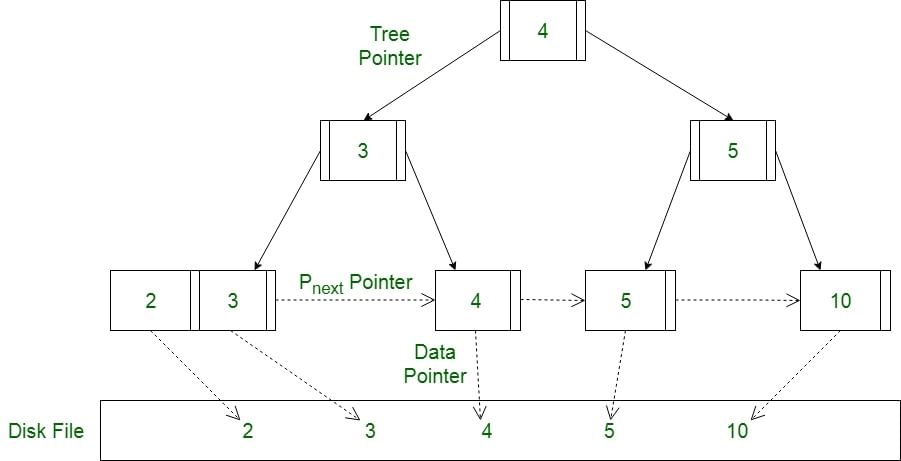 A Diagram of B+ Tree
A Diagram of B+ Tree
Insertion in a B+ tree
Prerequisite: Introduction of B+ trees
In this article, we will discuss that how to insert a node in B+ Tree. During insertion following properties of B+ Tree must be followed:
- Each node except root can have a maximum of M children and at least ceil(M/2) children.
- Each node can contain a maximum of M – 1 keys and a minimum of ceil(M/2) – 1 keys.
- The root has at least two children and atleast one search key.
- While insertion overflow of the node occurs when it contains more than M – 1 search key values.
Here M is the order of B+ tree.
Steps for insertion in B+ Tree
- Every element is inserted into a leaf node. So, go to the appropriate leaf node.
- Insert the key into the leaf node in increasing order only if there is no overflow. If there is an overflow go ahead with the following steps mentioned below to deal with overflow while maintaining the B+ Tree properties.
Properties for insertion B+ Tree
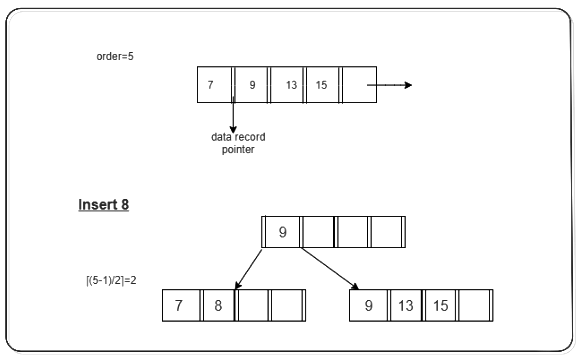
Case 1: Overflow in leaf node
- Split the leaf node into two nodes.
- First node contains ceil((m-1)/2) values.
- Second node contains the remaining values.
- Copy the smallest search key value from second node to the parent node.(Right biased)
Below is the illustration of inserting 8 into B+ Tree of order of 5:
Case 2: Overflow in non-leaf node
- Split the non leaf node into two nodes.
- First node contains ceil(m/2)-1 values.
- Move the smallest among remaining to the parent.
- Second node contains the remaining keys.
Below is the illustration of inserting 15 into B+ Tree of order of 5:
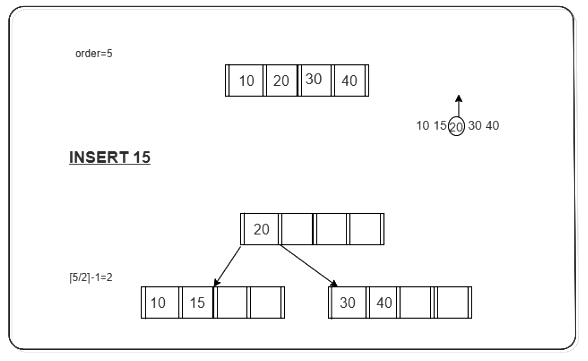
Example to illustrate insertion on a B+ tree
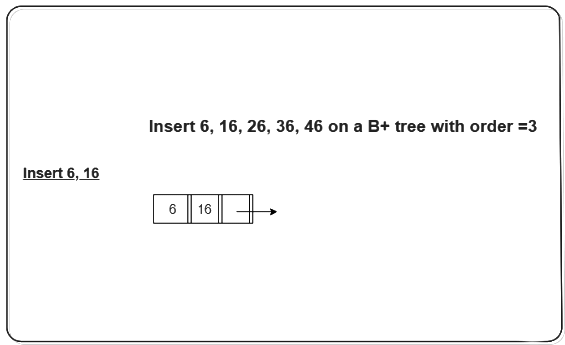
Problem: Insert the following key values 6, 16, 26, 36, 46 on a B+ tree with order = 3.
Sol:
Step 1: The order is 3 so at maximum in a node so there can be only 2 search key values. As insertion happens on a leaf node only in a B+ tree so insert search key value 6 and 16 in increasing order in the node. Below is the illustration of the same:
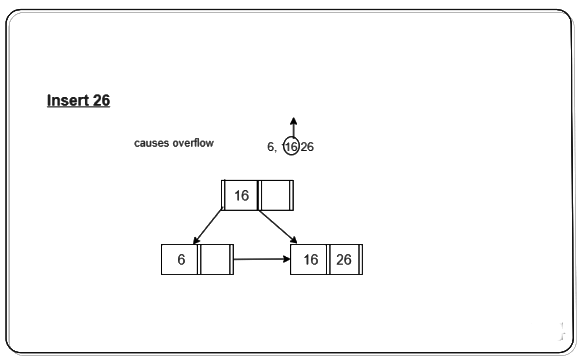
Step 2: We cannot insert 26 in the same node as it causes an overflow in the leaf node, We have to split the leaf node according to the rules. First part contains ceil((3-1)/2) values i.e., only 6. The second node contains the remaining values i.e., 16 and 26. Then also copy the smallest search key value from the second node to the parent node i.e., 16 to the parent node. Below is the illustration of the same:
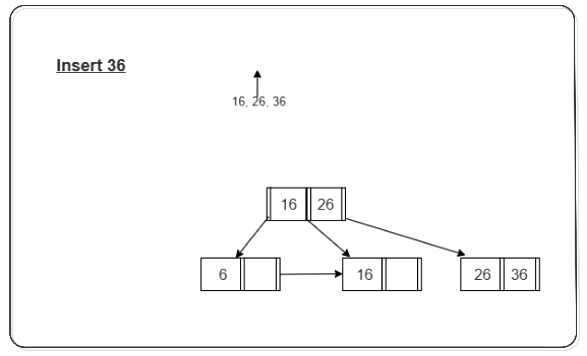
Step 3: Now the next value is 36 that is to be inserted after 26 but in that node, it causes an overflow again in that leaf node. Again follow the above steps to split the node. First part contains ceil((3-1)/2) values i.e., only 16. The second node contains the remaining values i.e., 26 and 36. Then also copy the smallest search key value from the second node to the parent node i.e., 26 to the parent node. Below is the illustration of the same:
The illustration is shown in the diagram below.
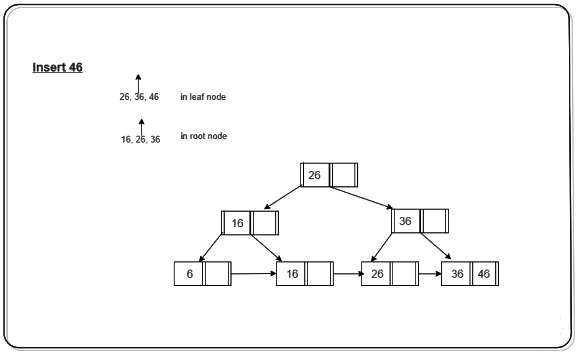
Step 4: Now we have to insert 46 which is to be inserted after 36 but it causes an overflow in the leaf node. So we split the node according to the rules. The first part contains 26 and the second part contains 36 and 46 but now we also have to copy 36 to the parent node but it causes overflow as only two search key values can be accommodated in a node. Now follow the steps to deal with overflow in the non-leaf node.
First node contains ceil(3/2)-1 values i.e. ’16’.
Move the smallest among remaining to the parent i.e ’26’ will be the new parent node.
The second node contains the remaining keys i.e ’36’ and the rest of the leaf nodes remain the same. Below is the illustration of the same:
Time Complexity:
- Insertion: O(log (h*bucketSize)), where h is height of the tree, and bucketSize denotes the number of elements that can be stored in a single bucket.
- Deletion: O(log (h*bucketSize))
Auxiliary Space: O(n), n-> number of elements in the tree.
Advantage
A B+ tree with ‘l’ levels can store more entries in its internal nodes compared to a B-tree having the same ‘l’ levels. This accentuates the significant improvement made to the search time for any given key. Having lesser levels and presence of Pnext pointers imply that B+ tree are very quick and efficient in accessing records from disks.
|
62 videos|99 docs|35 tests
|
FAQs on B + Tree - Database Management System (DBMS) - Computer Science Engineering (CSE)
| 1. What is a B+ Tree? |  |
| 2. How does a B+ Tree differ from a B-Tree? |  |
| 3. What is the purpose of using a B+ Tree in database systems? |  |
| 4. How is a B+ Tree structured? |  |
| 5. What are the benefits of using a B+ Tree over other data structures? |  |
















