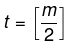B - Tree | Database Management System (DBMS) - Computer Science Engineering (CSE) PDF Download
Introduction
B-Tree is a self-balancing search tree. In most of the other self-balancing search trees (like AVL and Red-Black Trees), it is assumed that everything is in main memory. To understand the use of B-Trees, we must think of the huge amount of data that cannot fit in main memory. When the number of keys is high, the data is read from disk in the form of blocks. Disk access time is very high compared to the main memory access time. The main idea of using B-Trees is to reduce the number of disk accesses. Most of the tree operations (search, insert, delete, max, min, ..etc ) require O(h) disk accesses where h is the height of the tree. B-tree is a fat tree. The height of B-Trees is kept low by putting maximum possible keys in a B-Tree node. Generally, the B-Tree node size is kept equal to the disk block size. Since the height of the B-tree is low so total disk accesses for most of the operations are reduced significantly compared to balanced Binary Search Trees like AVL Tree, Red-Black Tree, ..etc.
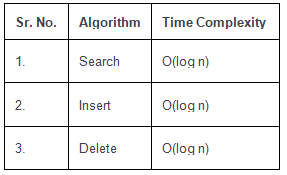
Time Complexity of B-Tree
“n” is the total number of elements in the B-tree.
Properties of B-Tree
- All leaves are at the same level.
- A B-Tree is defined by the term minimum degree ‘t’. The value of t depends upon disk block size.
- Every node except root must contain at least (ceiling)([t-1]/2) keys. The root may contain minimum 1 key.
- All nodes (including root) may contain at most t – 1 keys.
- Number of children of a node is equal to the number of keys in it plus 1.
- All keys of a node are sorted in increasing order. The child between two keys k1 and k2 contains all keys in the range from k1 and k2.
- B-Tree grows and shrinks from the root which is unlike Binary Search Tree. Binary Search Trees grow downward and also shrink from downward.
- Like other balanced Binary Search Trees, time complexity to search, insert and delete is O(log n).
Following is an example of B-Tree of minimum order 5. Note that in practical B-Trees, the value of the minimum order is much more than 5.
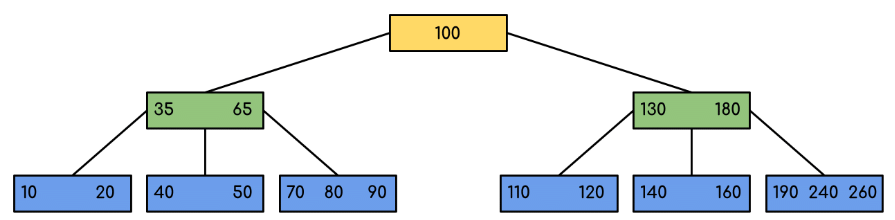
We can see in the above diagram that all the leaf nodes are at the same level and all non-leaf have no empty sub-tree and have keys one less than the number of their children.
Interesting Facts
- The minimum height of the B-Tree that can exist with n number of nodes and m is the maximum number of children of a node can have is:

- The maximum height of the B-Tree that can exist with n number of nodes and d is the minimum number of children that a non-root node can have is:
 and
and 
Traversel in B-Tree:
Traversal is also similar to Inorder traversal of Binary Tree. We start from the leftmost child, recursively print the leftmost child, then repeat the same process for remaining children and keys. In the end, recursively print the rightmost child.
Search Operation in B-Tree:
Search is similar to the search in Binary Search Tree. Let the key to be searched be k. We start from the root and recursively traverse down. For every visited non-leaf node, if the node has the key, we simply return the node. Otherwise, we recur down to the appropriate child (The child which is just before the first greater key) of the node. If we reach a leaf node and don’t find k in the leaf node, we return NULL.
Logic:
Searching a B-Tree is similar to searching a binary tree. The algorithm is similar and goes with recursion. At each level, the search is optimised as if the key value is not present in the range of parent then the key is present in another branch. As these values limit the search they are also known as limiting value or separation value. If we reach a leaf node and don’t find the desired key then it will display NULL.
Example: Searching 120 in the given B-Tree.
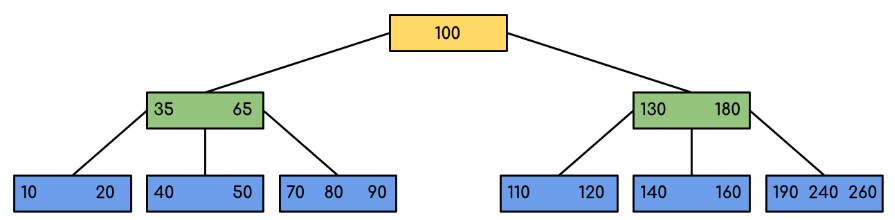
Solution:
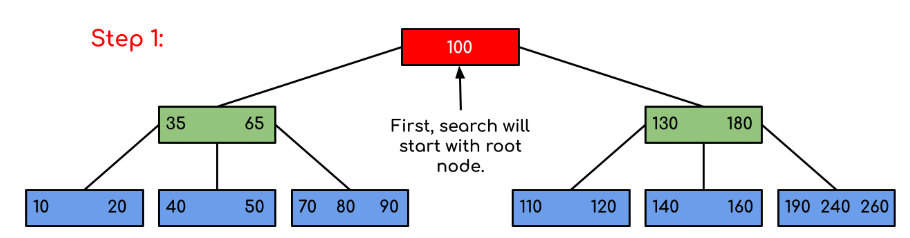
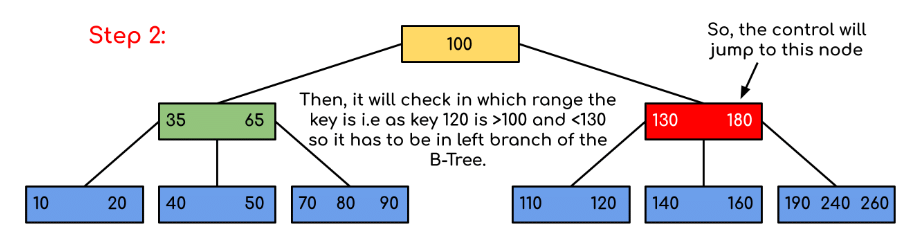
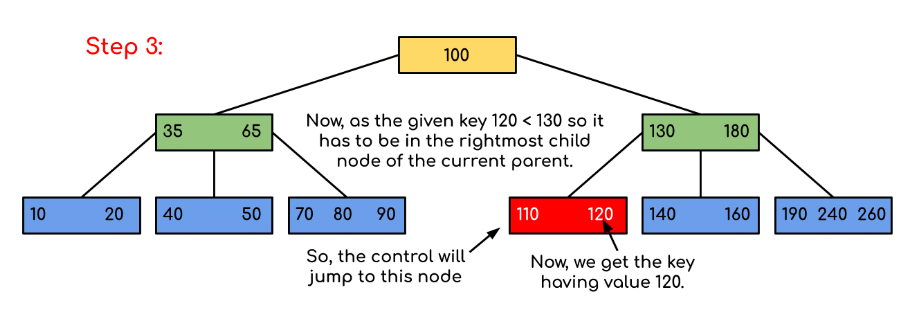
In this example, we can see that our search was reduced by just limiting the chances where the key containing the value could be present. Similarly if within the above example we’ve to look for 180, then the control will stop at step 2 because the program will find that the key 180 is present within the current node. And similarly, if it’s to seek out 90 then as 90 < 100 so it’ll go to the left subtree automatically and therefore the control flow will go similarly as shown within the above example.
Insert Operation in B-Tree
A new key is always inserted at the leaf node. Let the key to be inserted be k. Like BST, we start from the root and traverse down till we reach a leaf node. Once we reach a leaf node, we insert the key in that leaf node. Unlike BSTs, we have a predefined range on the number of keys that a node can contain. So before inserting a key to the node, we make sure that the node has extra space.
How to make sure that a node has space available for a key before the key is inserted? We use an operation called splitChild() that is used to split a child of a node. See the following diagram to understand split. In the following diagram, child y of x is being split into two nodes y and z. Note that the splitChild operation moves a key up and this is the reason B-Trees grow up, unlike BSTs which grow down.
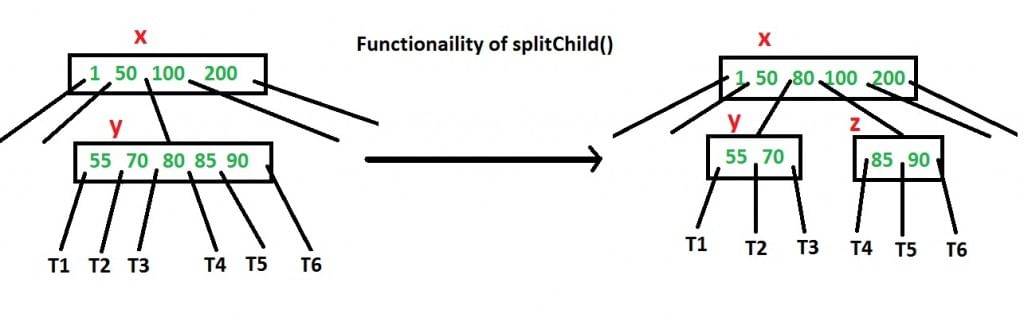
As discussed above, to insert a new key, we go down from root to leaf. Before traversing down to a node, we first check if the node is full. If the node is full, we split it to create space. Following is the complete algorithm.
Insertion
- Initialize x as root.
- While x is not leaf, do following
- Find the child of x that is going to be traversed next. Let the child be y.
- If y is not full, change x to point to y.
- If y is full, split it and change x to point to one of the two parts of y. If k is smaller than mid key in y, then set x as the first part of y. Else second part of y. When we split y, we move a key from y to its parent x.
- The loop in step 2 stops when x is leaf. x must have space for 1 extra key as we have been splitting all nodes in advance. So simply insert k to x.
Note that the algorithm follows the Cormen book. It is actually a proactive insertion algorithm where before going down to a node, we split it if it is full. The advantage of splitting before is, we never traverse a node twice. If we don’t split a node before going down to it and split it only if a new key is inserted (reactive), we may end up traversing all nodes again from leaf to root. This happens in cases when all nodes on the path from the root to leaf are full. So when we come to the leaf node, we split it and move a key up. Moving a key up will cause a split in parent node (because the parent was already full). This cascading effect never happens in this proactive insertion algorithm. There is a disadvantage of this proactive insertion though, we may do unnecessary splits.
Let us understand the algorithm with an example tree of minimum degree ‘t’ as 3 and a sequence of integers 10, 20, 30, 40, 50, 60, 70, 80 and 90 in an initially empty B-Tree.
Initially root is NULL. Let us first insert 10.
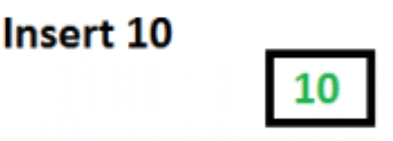
Let us now insert 20, 30, 40 and 50. They all will be inserted in root because the maximum number of keys a node can accommodate is 2*t – 1 which is 5.

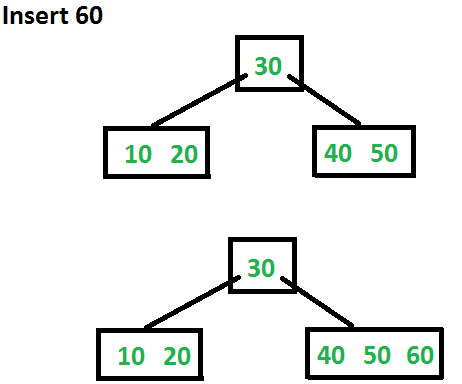
Let us now insert 60. Since root node is full, it will first split into two, then 60 will be inserted into the appropriate child.
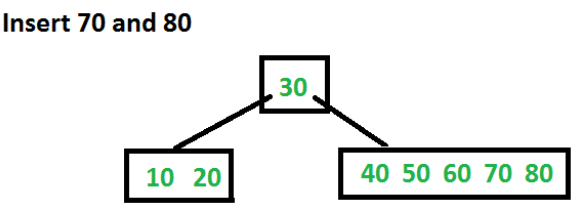
Let us now insert 70 and 80. These new keys will be inserted into the appropriate leaf without any split.
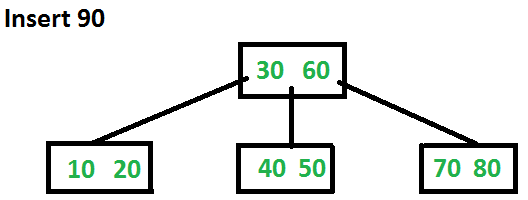
Let us now insert 90. This insertion will cause a split. The middle key will go up to the parent.
Delete Operation in B-Tree
Deletion process
Deletion from a B-tree is more complicated than insertion, because we can delete a key from any node-not just a leaf—and when we delete a key from an internal node, we will have to rearrange the node’s children.
As in insertion, we must make sure the deletion doesn’t violate the B-tree properties. Just as we had to ensure that a node didn’t get too big due to insertion, we must ensure that a node doesn’t get too small during deletion (except that the root is allowed to have fewer than the minimum number t-1 of keys). Just as a simple insertion algorithm might have to back up if a node on the path to where the key was to be inserted was full, a simple approach to deletion might have to back up if a node (other than the root) along the path to where the key is to be deleted has the minimum number of keys.
The deletion procedure deletes the key k from the subtree rooted at x. This procedure guarantees that whenever it calls itself recursively on a node x, the number of keys in x is at least the minimum degree t . Note that this condition requires one more key than the minimum required by the usual B-tree conditions, so that sometimes a key may have to be moved into a child node before recursion descends to that child. This strengthened condition allows us to delete a key from the tree in one downward pass without having to “back up” (with one exception, which we’ll explain). You should interpret the following specification for deletion from a B-tree with the understanding that if the root node x ever becomes an internal node having no keys (this situation can occur in cases 2c and 3b then we delete x, and x’s only child x.c1 becomes the new root of the tree, decreasing the height of the tree by one and preserving the property that the root of the tree contains at least one key (unless the tree is empty).
We sketch how deletion works with various cases of deleting keys from a B-tree:
- If the key k is in node x and x is a leaf, delete the key k from x.
- If the key k is in node x and x is an internal node, do the following.
- If the child y that precedes k in node x has at least t keys, then find the predecessor k0 of k in the sub-tree rooted at y. Recursively delete k0, and replace k by k0 in x. (We can find k0 and delete it in a single downward pass.)
- If y has fewer than t keys, then, symmetrically, examine the child z that follows k in node x. If z has at least t keys, then find the successor k0 of k in the subtree rooted at z. Recursively delete k0, and replace k by k0 in x. (We can find k0 and delete it in a single downward pass.)
- Otherwise, if both y and z have only t-1 keys, merge k and all of z into y, so that x loses both k and the pointer to z, and y now contains 2t-1 keys. Then free z and recursively delete k from y.
- If the key k is not present in internal node x, determine the root x.c(i) of the appropriate subtree that must contain k, if k is in the tree at all. If x.c(i) has only t-1 keys, execute step 3a or 3b as necessary to guarantee that we descend to a node containing at least t keys. Then finish by recursing on the appropriate child of x.
- If x.c(i) has only t-1 keys but has an immediate sibling with at least t keys, give x.c(i) an extra key by moving a key from x down into x.c(i), moving a key from x.c(i) ’s immediate left or right sibling up into x, and moving the appropriate child pointer from the sibling into x.c(i).
- If x.c(i) and both of x.c(i)’s immediate siblings have t-1 keys, merge x.c(i) with one sibling, which involves moving a key from x down into the new merged node to become the median key for that node.
Since most of the keys in a B-tree are in the leaves, deletion operations are most often used to delete keys from leaves. The recursive delete procedure then acts in one downward pass through the tree, without having to back up. When deleting a key in an internal node, however, the procedure makes a downward pass through the tree but may have to return to the node from which the key was deleted to replace the key with its predecessor or successor (cases 2a and 2b).
The following figures explain the deletion process:
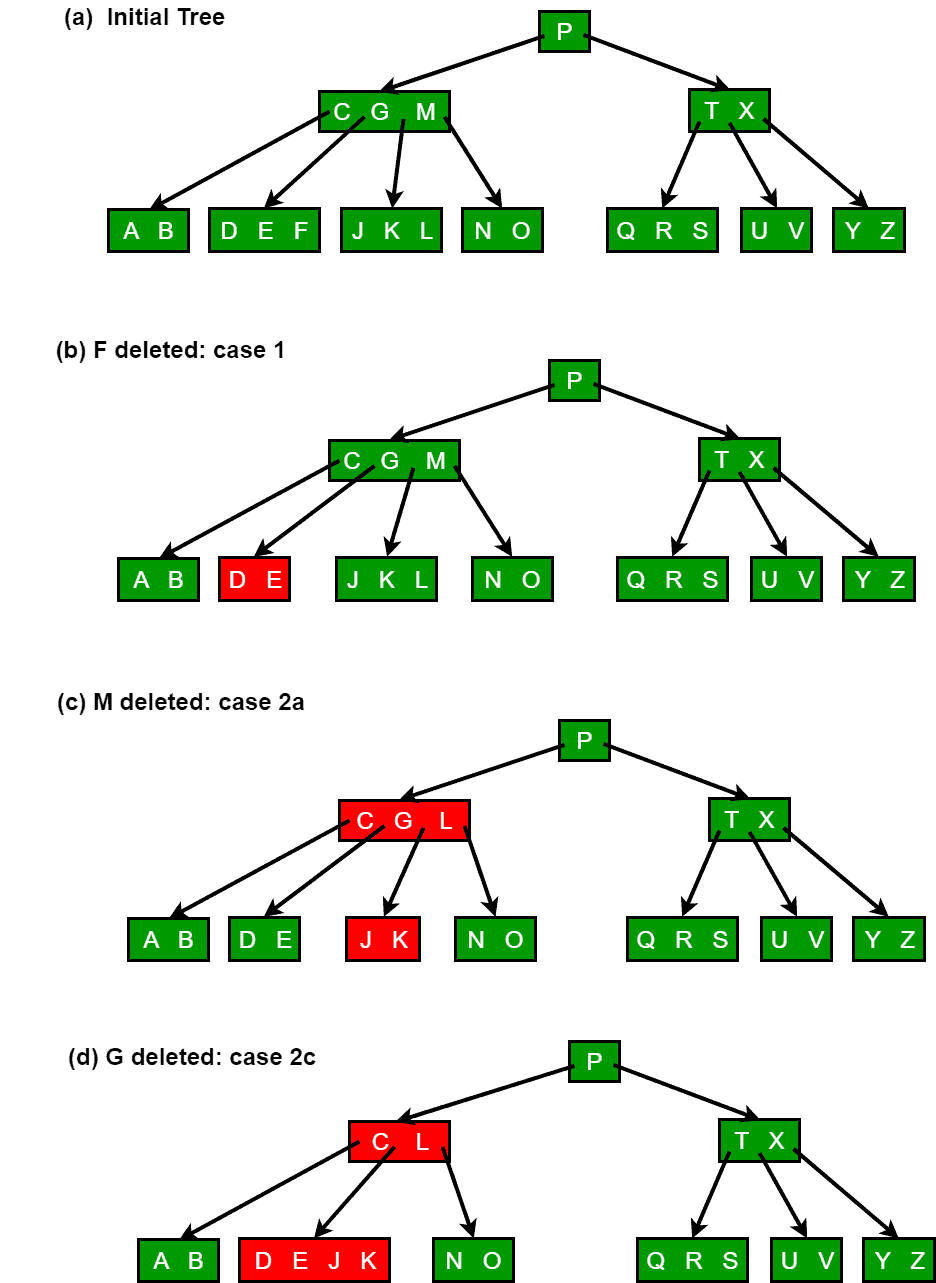
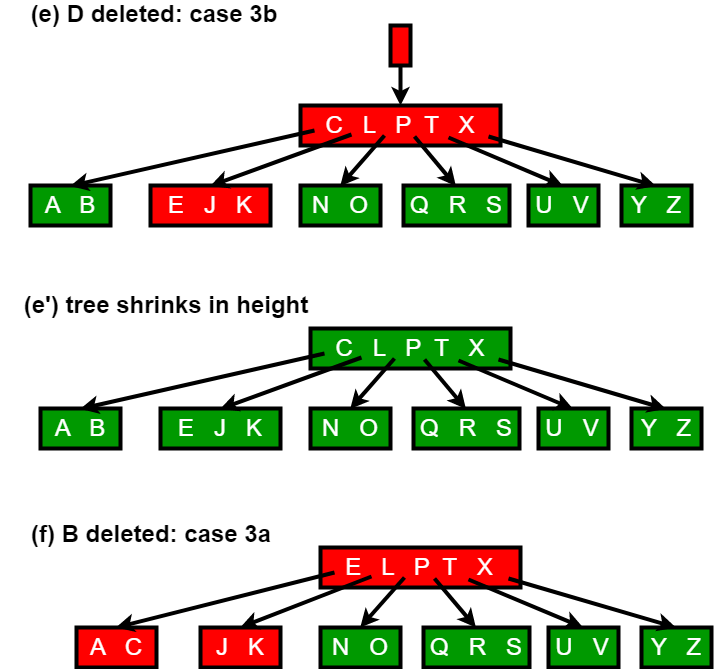
|
62 videos|66 docs|35 tests
|
FAQs on B - Tree - Database Management System (DBMS) - Computer Science Engineering (CSE)
| 1. What is a B-Tree? |  |
| 2. How does the insert operation work in a B-Tree? |  |
| 3. What is the complexity of the insert operation in a B-Tree? |  |
| 4. How does the delete operation work in a B-Tree? |  |
| 5. What is the complexity of the delete operation in a B-Tree? |  |

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
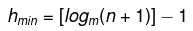
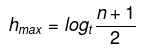 and
and