Base Systems | Quantitative Aptitude (Quant) - CAT PDF Download
Introduction
- The numbers that we commonly use are the decimal number. The system is called the decimal system. Why is it called the decimal system? It is because it has 10 symbols : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Example: 85 means: 8 * 101 + 5 * 100 - Here, 10 is known as the base of the decimal system.
- Base: It is the number of distinct symbols used in a particular number system.
So, depending on the number of digits in the base system, there are many other systems possible. Have a look at the following table: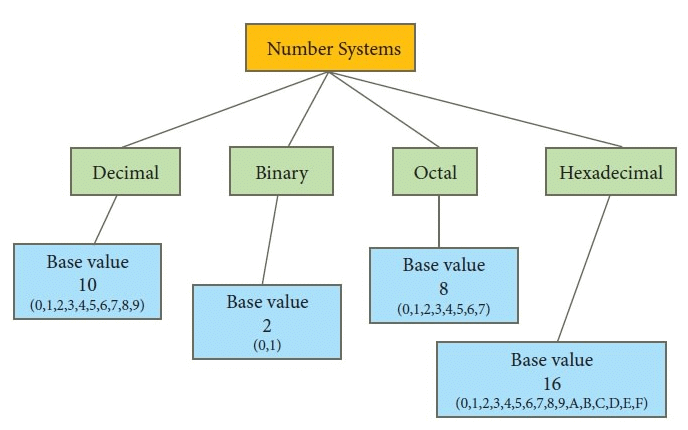 Classification of Number System
Classification of Number System - In the questions involving base systems, we are expected to figure out the different numbers of digits in that system of counting.
- Example: If we had 7 digits instead of 10 i.e. 0, 1, 2, 3, 4, 5, 6, we would have a system of counting as follows: 0, 1, 2, 3, 4, 5, 6, 10, 11, 12, 13, 14… .
In above system , 45 will be expanded as = 6 * 71 + 3* 90
Questions in MBA entrance exams are based on two concepts:
1. Conversion of numbers from one base system to another.
2. Arithmetic Operations of numbers in any base system.
Conversions From One Base System to Another
1. Decimal to Binary
(a) (10.25)10
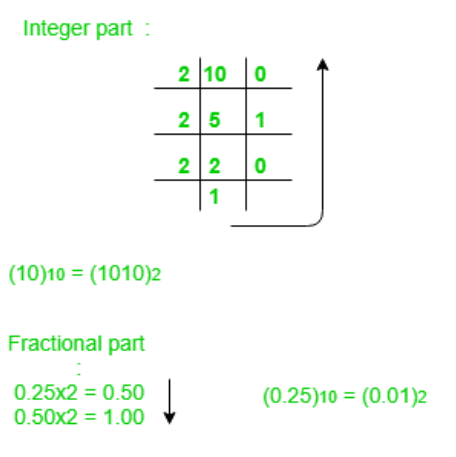
Note: Keep multiplying the fractional part with 2 until decimal part 0.00 is obtained.
(0.25)10 = (0.01)2
Answer: (10.25)10 = (1010.01)2
(b) (28.3125)10
The given number has 2 parts:
(i) Conversion of an integral part:
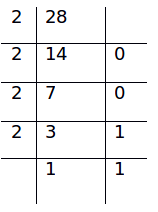
(28)10 = (11100)2
(ii) Conversion of the fractional part:
- Multiply the decimal part with 2 successively and take the integral part of all the products starting from the first.
- 0.3125*2 = 0.6250 → (0)
- 0.6250*2 = 1.2500 → (1)
- 0.2500*2 = 0.500 → (0)
- 0.500*2 = 1 → (1)
- Therefore,
- (0.3125)10 = (0.0101)2
- (28.3125)10 = (11100.0101)2
Note: We should stop multiplying the factorial part by 2, once we get 0 as a fraction or the fractional part is non-terminating. It can be decided depending on the number of digits in the fractional part required.
2. Binary to Decimal
- (110101)2 = 1*25+ 1*24+ 0*23+ 1*22+ 0*21+ 1*20 = (53)10
- (0.11001)2 = 1*2-1+ 1*2-2+ 0*2-3+ 0*2-4+ 1*2-5 = (0.78125)10Question for Base SystemsTry yourself:Convert the binary equivalent 10101 to its decimal equivalent.View Solution
3. Decimal to Octal
(a) (4324.235)10
(i) Integral Part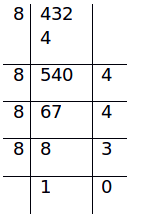
(4324)10 = (10344)8
(ii) Fractional Part
- 0.235*8 = 1.88 → (1)
- 0.88*8 = 7.04 → (7)
- 0.04*8 = 0.32 → (0)
- We can stop here as the fraction is non-terminating.
- (4324.235)10 = (10344.170)8
4. Octal to Decimal
- (677.47)8
= 6*82+ 7*81+ 7*80+ 4*8-1+ 7*8-2 = (447.609375)10
5. Decimal to Hexadecimal
- (23524)10

(23524)10 = (5BE4)16
6. Hexadecimal to Decimal
- (62A)16 = 6*162+ 2*161+ 10*160 = (1578)10
Now, we will look at conversions which do not include base 10. We can observe that the following cases include 2 bases (let them be a and b), where a=bn.
7. Binary to Octal
- (octal) is a cube of 2 (binary). So, to convert binary to octal, we just need to club three digits of binary number starting from unit digit and write the decimal equivalent of each group.
- (1101001011)2 = (001 101 001 011)2
(We can introduce two zeroes to form groups of 3 without changing the magnitude of the number)
(001 101 001 011)2 = (1513)8
8. Octal to Binary
Here, we need to express every digit of octal number into its binary form comprising of 3 digits.
- (645)8
- 6 = (110)2
- 4 = (100)2
- 5 = (101)2
- (645)8 = (110 100 101)2
9. Binary to Hexa-Decimal
- It is similar to the method discussed in the 7th point. Instead of clubbing 3, we club 4 digits.
- (10101110)2 = (1010 1110)2 = (AE)16
10. Hexa-Decimal to Binary
- We need to express every digit of Hexa-decimal into its binary form comprising of 4 digits.
- (3A91)16
- 3 = (0011)2
- A = (1010)2
- 9 = (1001)2
- 1 = (0001)2
- (3A91)16 = (11101010010001)2
Note: Using the logic discussed in points 7 to 10, we can do direct conversions in any two bases a and b such that a=bn where we will form blocks of n digits when the number is in base b and then write its decimal equivalent.
Example: For conversion from base 3 to base 9, we need to make blocks of 2 digits as 9 = 32, for instance- (22112)3 = (02 21 12)3 = (275)9
Arithmetic Operations While Operating in a Specific Base System
- One method of performing arithmetic operations is to first convert the numbers to the decimal system, perform the required operations and then convert the numbers back to the required base.
- However, arithmetic operations can also be directly done given that numbers are expressed in the same base.
1. Addition
Let us start with an easy example to understand the rationale.
(a) (8358)10 + (5684)10
(8358)10 + (5684)10 = (14042)10
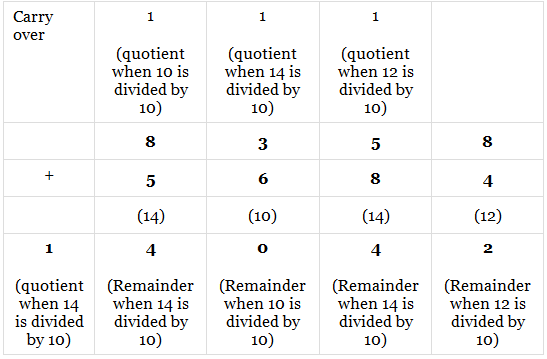
➢ Logic
- Start from a unit position; 8+4=12, and 12, when divided by 10 (base), gives us remainder as 2, which is the total for that column. 12, when divided by 10, gives us quotient as 1, which is carried over to the next column.
- In the second column, 1+5+8=14. When 14 is divided by 10 (base), we get 4 as remainder (total for that column) and 1 as quotient which is carried over to next column.
- In third column, 1 + 3 + 6 = 10. 10, when divided by 10, gives us 0 as remainder and 1 as quotient. We proceed in similar and get the required sum.
(b) (3542)6 + (4124)6
(3542)6 + (4124)6 = (12110)6
2. Subtraction
(a) (237)10 – (199)10
(237)10 – (199)10 = (38)10

➢ Logic
- In units place 7 < 9, hence we borrow 10 (base) from tens place. 17-9=8
- Tens place reduces from 3 to 2. Still 2<9, hence we borrow 10 (base) from hundreds place. 12-9=3
- Hundreds place reduces to 1 (as we borrowed from it in an earlier step). 1-1=0
(b) (422)5 – (243)5
(422)5 – (243)5 = (124)5
3. Multiplication
For multiplying numbers in any base system, multiply them as we normally do for decimal numbers and while writing, write each number in the given base system
Example: Calculate (52)8 × (6)8
Solution:
Given, (52)8 × (6)8
We first multiply 6 with 2 i.e., 2 × 6 = 12 and write it in base 8 = (14)8.
Now, 4 will be the unit's digit of the final answer and 1 will be carried forward.
Now we multiply 6 with 5 and add any carry forward i.e., 5 × 6 + 1 = 31 and write it in base 8 = (37)6
Now, 37 will be the leftmost digit of the final answer.
∴ (52)8 × (6)8 = (374)8
4. Division
- Division of a number in base n by (n - 1)
(x)n is divisible by (n - 1) if the sum of all the digits of (x)n is divisible by (n - 1) - Division of a number in base n by (n + 1)
(x)n is divisible by (n + 1) if the difference of the sums of alternate digits of (x)n is either 0 or divisible by (n + 1) - Number of zeroes at the end of a number in base n
For a number in base n, if there are k zeroes in the end then it is divisible by nk. Also, k is the highest power of n in the number.
(a) Is (7364)9 divisible by 8?
- The logic behind this question is same as checking the divisibility of any number (in decimal system) by 9. We add the digits and then check the divisibility.
7 + 3 + 6 + 4 = 20 which is not divisible by 8. Hence, the given number is not divisible by 8.
Rule: (x)b is divisible by (b-1) if all the digits of (x)b add up to be divisible by (b-1).
(b) Is (5236)9 divisible by 10?
- The logic behind this question is same as checking the divisibility of any number (in decimal system) by 11.
- We first find the sum of alternate digits and then find the difference of the sums obtained. This difference should either be divisible by 0 or divisible by 11(or 10 in the case of this question).
- 5 + 3 = 8; 2 + 6 = 8
- 8 - 8 = 0. Hence, the number is divisible by 10.
Rule: (x)b is divisible by (b+1) if the difference of the sums of alternate digits of (x)b is either 0 or divisible by (b+1).
(c) What is the IGP (Index of Greatest Power) of 9 in (780)9?
- (780)9 = 7*92+ 8*91+ 0*90 = 9(7*9+ 8)
- Thus IGP= 1. As the highest power of 9 with which the number is divisible is 1.
Rule: For a number in base b, if there are k zeroes in the end then it is divisible by bk. Also, k is the IGP of b in the number.
Important Concepts of Base System
Example 1. Find the fifth root of (15AA51)19
- (15AA51)19 = 1*195+ 5*194+ 10*193+ 10*192+ 5*191+ 1*190 = (19+1)5 = 205 (Using binomial theorem)
- Therefore, the fifth root is 20.
Other examples of similar kind are:
- (121)n = n2+ 2n+ 1= (n+1)2 (n>2)
- (1331)n = n3+ 3n2+ 3n+ 1= (n+1)3 (n>3)
- (14641)n, (15AA51)n and so on (the digits of the numbers used in the above examples form Pascal’s triangle)
Example 2. How many 4-digit numbers in base 9 are perfect squares?
- First, we need to know the range of 4-digit numbers in base 9
Least 4 digit number possible= (1000)9 = 93 =729
- Observation: Lowest n digit number in base k = k(n-1)
Highest 4 digit number possible= (8888)9 = 94-1= 6560
- Observation: Highest n digit number in base k = kn-1
- From 729 to 6560, the squares vary from 272 to 802.
- Number of perfect squares present = 80 - 26 = 54.
Previous Year Questions based on Base System
Q.1. Let a, b, c be distinct digits. Consider a two-digit number ‘ab’ and a three-digit number ‘ccb’, both defined under the usual decimal number system, if (ab)2 = ccb > 300, then the value of b is? (CAT 1999)(a) 1
(b) 0
(c) 5
(d) 6
Correct Answer is Option (a).
- (ab)2 = ccb, the greatest possible value of ‘ab’ can be 31, since 312 = 961 (and since ccb > 300), 300 < ccb < 961, so 18 < ab < 31.
- So the possible value of ab which satisfies (ab)2 = ccb is 21.
- So 212 = 441, ∴ a = 2, b = 1, c = 4.
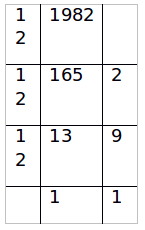
Q.2. Convert the number 1982 from base 10 to base 12. The result is? (CAT 2000)
(a) 1182
(b) 1912
(c) 1192
(d) 1292
Correct Answer is Option (c).
Q.3. In a number system, the product of 44 and 11 is 1034. The number 3111 of this system, when converted to the decimal number system, becomes? (XAT 2001)
(a) 406
(b) 1086
(c) 213
(d) 691
(e) None of the above
Correct Answer is Option (a).
- Let the base be n
- (4n+4)(n+1) = n3+3n+4
- n3-4n2-5n = 0
- n(n-5)(n+1) = 0
- n = 5
- (3111)5 = (406)10
Q.4: What will be the number of zeroes in ( 2000 ! ) 34 .
Here 34 is the base in which the number is written.
a) 122
b)123
c)124
d)125
Correct answer is option (b)34 = 17*2
So we have to find the highest power of 17 in 2000!. We need not find the power of 2 because power of 2 will be greater than the power of 17.
Thus, the power of 17 will act as a limiting value.
Thus, the highest power of 17 in 2000! is
[2000/17] + [2000/289] + [2000/4913], [] is greatest integer function.
= 117 + 6 + 0 = 123
Thus, the required number of zeroes is 123
|
184 videos|212 docs|103 tests
|
FAQs on Base Systems - Quantitative Aptitude (Quant) - CAT
| 1. What are some common base systems used in mathematics and computer science for representing numbers? |  |
| 2. How can one convert a number from decimal to binary? |  |
| 3. What is the significance of the base system in computer programming and digital electronics? |  |
| 4. How can arithmetic operations like addition and multiplication be performed in a specific base system? |  |
| 5. What are some key concepts to understand when working with different base systems in mathematics and computer science? |  |