In this chapter we will be looking exclusively at linear second order differential equations. The most general linear second order differential equation is in the form.
...(1.)
In fact, we will rarely look at non-constant coefficient linear second order differential equations. In the case where we assume constant coefficients we will use the following differential equation.
...(2.)
Where possible we will use (1) just to make the point that certain facts, theorems, properties, and/or techniques can be used with the non-constant form. However, most of the time we will be using (2) as it can be fairly difficult to solve second order non-constant coefficient differential equations.
Initially we will make our life easier by looking at differential equations with g(t)=0. When g(t)=0 we call the differential equation homogeneous and when g(t)≠0 we call the differential equation nonhomogeneous.
So, let’s start thinking about how to go about solving a constant coefficient, homogeneous, linear, second order differential equation. Here is the general constant coefficient, homogeneous, linear, second order differential equation.
It’s probably best to start off with an example. This example will lead us to a very important fact that we will use in every problem from this point on. The example will also give us clues into how to go about solving these in general.
Example 1: Determine some solutions to
Solution: We can get some solutions here simply by inspection. We need functions whose second derivative is 9 times the original function. One of the first functions that I can think of that comes back to itself after two derivatives is an exponential function and with proper exponents the 9 will get taken care of as well.
So, it looks like the following two functions are solutions.
We’ll leave it to you to verify that these are in fact solutions.
These two functions are not the only solutions to the differential equation however. Any of the following are also solutions to the differential equation.
In fact if you think about it any function that is in the form
will be a solution to the differential equation.
This example leads us to a very important fact that we will use in practically every problem in this chapter.
Principle of Superposition
If y1(t) and y2(t) are two solutions to a linear, homogeneous differential equation then so is
y(t)=c1y1(t)+c2y2(t) ...(3.)
Note that we didn’t include the restriction of constant coefficient or second order in this. This will work for any linear homogeneous differential equation.
If we further assume second order and one other condition (which we’ll give in a second) we can go a step further.
If y1(t) and y2(t) are two solutions to a linear, second order homogeneous differential equation and they are “nice enough” then the general solution to the linear, second order homogeneous differential equation is given by (3).
So, just what do we mean by “nice enough”? We’ll hold off on that until a later section. At this point you’ll hopefully believe it when we say that specific functions are “nice enough”.
So, if we now make the assumption that we are dealing with a linear, second order homogeneous differential equation, we now know that (3) will be its general solution. The next question that we can ask is how to find the constants c1 and c2. Since we have two constants it makes sense, hopefully, that we will need two equations, or conditions, to find them.
One way to do this is to specify the value of the solution at two distinct points, or,
These are typically called boundary values and are not really the focus of this course so we won’t be working with them here. We do give a brief introduction to boundary values in a later chapter if you are interested in seeing how they work and some of the issues that arise when working with boundary values.
Another way to find the constants would be to specify the value of the solution and its derivative at a particular point. Or,
These are the two conditions that we’ll be using here. As with the first order differential equations these will be called initial conditions.
Example 2: Solve the following IVP.
Solution: First, the two functions
are “nice enough” for us to form the general solution to the differential equation. At this point, please just believe this. You will be able to verify this for yourself in a couple of sections.
The general solution to our differential equation is then
Now all we need to do is apply the initial conditions. This means that we need the derivative of the solution.
Plug in the initial conditions
This gives us a system of two equations and two unknowns that can be solved. Doing this yields
The solution to the IVP is then,
Up to this point we’ve only looked at a single differential equation and we got its solution by inspection. For a rare few differential equations we can do this. However, for the vast majority of the second order differential equations out there we will be unable to do this.
So, we would like a method for arriving at the two solutions we will need in order to form a general solution that will work for any linear, constant coefficient, second order homogeneous differential equation. This is easier than it might initially look.
We will use the solutions we found in the first example as a guide. All of the solutions in this example were in the form
Note, that we didn’t include a constant in front of it since we can literally include any constant that we want and still get a solution. The important idea here is to get the exponential function. Once we have that we can add on constants to our hearts content.
So, let’s assume that all solutions to
...(4.)
...(5.)
To see if we are correct all we need to do is plug this into the differential equation and see what happens. So, let’s get some derivatives and then plug in.
So, if (5) is to be a solution to (4) then the following must be true
This can be reduced further by noting that exponentials are never zero. Therefore, (5) will be a solution to (4)provided r is a solution to
...(6.)
This equation is typically called the characteristic equation for (4).
Okay, so how do we use this to find solutions to a linear, constant coefficient, second order homogeneous differential equation? First write down the characteristic equation, (6), for the differential equation, (4). This will be a quadratic equation and so we should expect two roots, r1 and r2. Once we have these two roots we have two solutions to the differential equation.
...(7.)
Let’s take a look at a quick example.
Example 3: Find two solutions to
Solution: This is the same differential equation that we looked at in the first example. This time however, let’s not just guess. Let’s go through the process as outlined above to see the functions that we guess above are the same as the functions the process gives us.
First write down the characteristic equation for this differential equation and solve it.
The two roots are 3 and -3. Therefore, two solutions are
These match up with the first guesses that we made in the first example.
You’ll notice that we neglected to mention whether or not the two solutions listed in (7) are in fact “nice enough” to form the general solution to (4).This was intentional. We have three cases that we need to look at and this will be addressed differently in each of these cases.
So, what are the cases? As we previously noted the characteristic equation is quadratic and so will have two roots, r1 and r2. The roots will have three possible forms. These are
1. Real, distinct roots,r1 ≠ r2.
2. Complex root,r1,2 = λ ± μi.
3. Double roots,r1 = r2 = r.
The next three sections will look at each of these in some more depth, including giving forms for the solution that will be “nice enough” to get a general solution.
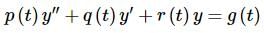...(1.)
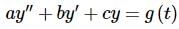...(2.)
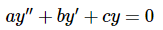...(4.)
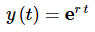...(5.)
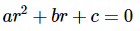...(6.)
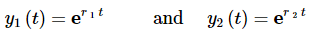...(7.)
