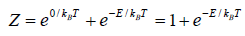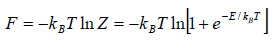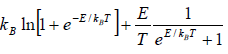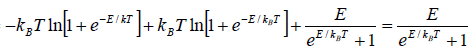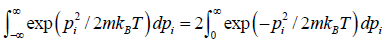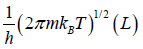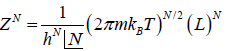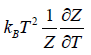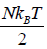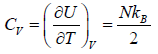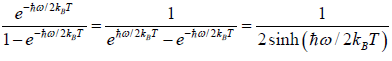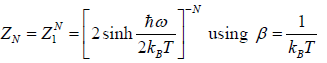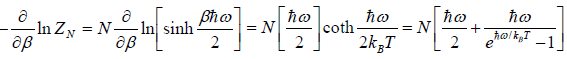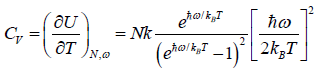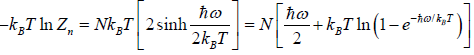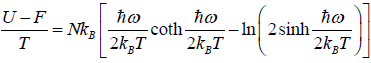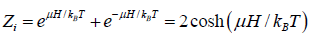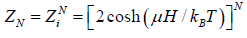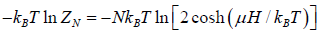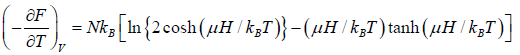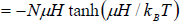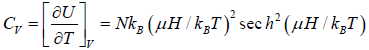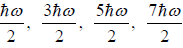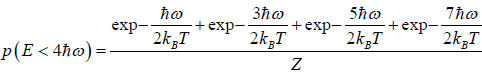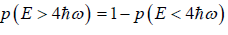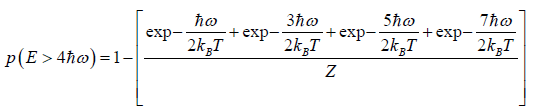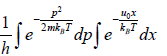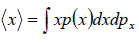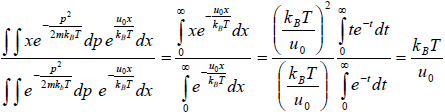Basic Definition & Postulates of Statistical Mechanics | Kinetic Theory & Thermodynamics - Physics PDF Download
Introduction
Statistical mechanics is a branch of physics that applies probability theory, which contains mathematical tools for dealing with large population, to study of the thermodynamic behavior of systems composed of a large number particles.
It provides a framework for relating the microscopic properties of individual atoms and molecules to the macroscopic bulk properties of materials that can be observed in everyday life.
- Micro state: A microstate is a specific microscopic configuration of a thermodynamic system that occupy with a certain property in the course of its thermal fluctuation. The position ( x ), momentum ( p ), energy ( E ), and spin ( s, sz ) of individual atom are the example of microstate of system.
- Macro state: A macro state refers to macroscopic properties of system such as temperature (T ), pressure ( P ), free energy ( F ), entropy ( S ). A macro state is characterized by a probability distribution of possible state across a certain statistical ensemble of all microstates, and distribution describes the probability of finding the system in certain microstate.
- Accessible state: Any microstate in which a system can be found without contradicting the macroscopic information available about the system.
- Statistical Ensemble: an assembly of large number of mutually non interacting systems, each of which satisfies the same conditions as those known to be satisfied by a particular system under condition. There are three type of ensemble (a) micro canonical ensemble, (b) canonical ensemble, (c) grand canonical ensemble. An ensemble is said to be time independent ensemble if number of system exhibiting any particular property is the same at a time.
- Probability: The probability pr of occurrence of an event r in a system is defined with respect to statistical ensemble of N such a systems. If Nr systems in the ensemble exhibit the event r then
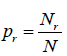
- Probability density: The probability density ρ (u) is defined by the property that ρ (u)du yields the probability of finding the continuous variable u in the range between u and u + du .
- Mean value: The mean value of u is denoted by (u) as defined as
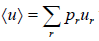 where the sum is over all possible value values ur of the variable u and pr is denotes the probability of occurrence of the particular value ur .Above definitionis for discrete variable. For continuous variable u
where the sum is over all possible value values ur of the variable u and pr is denotes the probability of occurrence of the particular value ur .Above definitionis for discrete variable. For continuous variable u 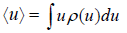
- Dispersions (or variance): The dispersion of u is defined as
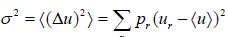 which is equivalent to
which is equivalent to 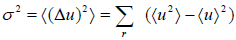
- Stirling formula: Stirling’s approximation (or Stirling’s formula) is an approximation for large factorials. It is named after James Stirling. The formula as typically used in applications is
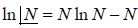
Postulates of statistical mechanics
If an isolated system is found with equal probability in each of its accessible state, it is in equilibrium, which is popularly known as postulates of equal a priori probabilities. Suppose that we were asked to pick a card at random from a well-shuffled pack. It is accepted that we have an equal probability of picking any card in the pack. There is nothing which would favor one particular card over all of the others. So, since there are fifty-two cards in a normal pack, we would expect the probability of picking the Ace of Spades, say, to be 1/52.
We could now place some constraints on the system. For instance, we could only count red cards, in which case the probability of picking the Ace of Hearts, say, would be 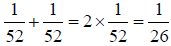 , by the same reasoning. In both cases, we have used the principle
, by the same reasoning. In both cases, we have used the principle
of equal a priori probabilities. People really believe that this principle applies to games
of chance such as cards, dice.
In statistical mechanics, we treat a many particle system a bit like an extremely large game of cards. Each accessible state corresponds to one of the cards in the pack. The
interactions between particles cause the system to continually change state. This is equivalent to constantly shuffling the pack. Finally, an observation of the state of the system is like picking a card at random from the pack. The principle of equal a priori probabilities then boils down to saying that we have an equal chance of choosing any particular card.
Example 1: If there are four identical molecule in one dimensional container and it is given that molecule can be found only either right or left end of container .
(a) What are possible configuration and no of ways to arrange these configuration? what are corresponding probability of each configuration?
(b) What is most probable configuration?
(c) If some one is doing the experiment in which he observed molecule position to right of container what is mean value of particle being in right?
(d) How postulates of a priori probability apply on the experiment?
The number of different ways of arranging N molecules with n on one side
and N - n on the other side is given by
, where ! represents the factorial function. The total number of possible ways of arranging the molecules is
(a)
(b) Most probable configuration is the one in which half the molecules are on one side and half on the other, i.e. the molecules are uniformly distributed over the space. Most probable configuration is configuration ( L, L ) and ( R, R ) which has maximum probability.
(c)
(d) We will now apply a fundamental postulate of statistical mechanics which states that an isolated system which can be in any one of a number of accessible states (=16 in this example) is equally likely to be in any one of these states at equilibrium. Therefore, the probability that the molecules are distributed in any one of these 16 possible ways is simply 1/16 . But there are 4 ways in which the molecules can be arranged so that 3 are on the left side and 1 on the right side, and therefore, the probability of finding that configuration is 4/16 . Similarly, other configuration can be weighted.
Example 2: Suppose we know 3 particle being spin 1/2 kept into homogeneous magnetic field B at temperature T .
(a) Show all possible microstate and corresponding probability .
(b) Find average value of z component of spin.
(c) If μ0 is magnetic moment which configuration has maximum energy what is corresponding probability.
(a) There is total 8 microstate is possible they are
(b) Average value of
(c) The energy is given by E = -μ0B the magnetic moment of configuration in which all three are down ↓↓↓ have magnetic moment - 3μ0 so this configuration has maximum energy which is equal to 3μ0B the corresponding probability is given by 1/8
Ensemble is collection of particle
Micro canonical ensemble
Micro canonical ensemble is theoretical tool used to analyze an isolated thermo dynamic system. The microstate of the system has fixed given energy (E), fixed number of particle (N)and fixed volume (V).All accessible micro state has same probability .
Popularly it is known as NVE ensemble.
Schematically the system can be shown as
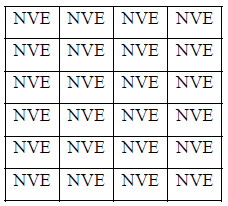
In above table each cell consider as each microstate. Energy, volume and no of particle is fixed in each cell.
If Ω is the number of accessible microstates, the probability that a system chosen at
random from the ensemble would be in a given microstate is simply 1/Ω.
No. of accessible microstate in phase space which has energy between E to E + dE is given by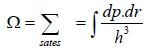 which is given in term of energy is
which is given in term of energy is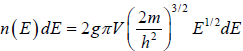 where g is degeneracy of the particle.
where g is degeneracy of the particle.
Entropy
From the number of accessible microstates, Ω , we can obtain the entropy (S) of the
system via ln , where 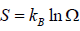 , where kB is the Boltzmann constant. or, equivalently,
, where kB is the Boltzmann constant. or, equivalently,
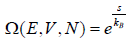 Ω is equivalent to “micro canonical partition function”
Ω is equivalent to “micro canonical partition function”
Example 3: If there is N number of particle which have spin 3//2 which will interact with magnetic field B which are in equilibrium at temperature T
(a) How many no. of microstate for each particle
(b) What is entropy of the system.
(a) if 3/2 s then z component of spin i.e. sz =
so there is 4
microstate for each particle
For the N no. of particle there will be 4N no of state.
(b) S = kB InΩ , where Ω = 4N for given system. So S = NkBIn4
Example 4: A solid contain N magnetic atoms having spin 1/2. At sufficiently high temperature each spin is completely random oriented. At sufficiently low temperature all the spin become oriented in same direction let the heat capacity as a function of temperature T by
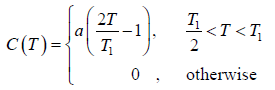
Find the value of "a"
at very low temperature all spins are oriented in only one direction so there is
only one possible microstate for each atoms . hence entropy isS1 = 0, at high temperature all the spin are randomly oriented and they can be either in up or down microstate so there are two microstate for each atom hence for N no of atom entropy is given by
S2 = NkB In 2
so S2 - S1 = NkB In 2 which is determined by theoretical calculation . now from the given expression of heat capacity we have relation c =
.
=
Canonical Ensemble
The canonical ensemble occurs when a system with fixed volume (V) and number of particle (N) at constant temperature (T) . In other words we will consider an assembly of systems closed to others by rigid, diathermal, impermeable walls. The energy of the
microstates can be fluctuate, the system is kept in equilibrium by being in contact with the heat bath at temperature T . It is also referred to as the NVT ensemble
Schematically the system can be shown as
In above table each cell considers as each microstate temperature, volume and number of particle is fixed in each cell. Only value of energy is different in different cell which can be exchanged in the process.
Partition Function for Canonical Ensemble
According to Gibbs, the probability of finding the system in any of its ith state at temperature T where energy of that state is Ei is given by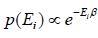 where
where 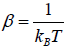
 where c is proportionality constant. Hence p(Ei) is probability then
where c is proportionality constant. Hence p(Ei) is probability then
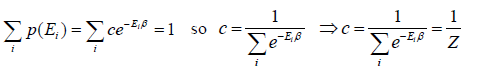
The letter Z stands for the German word Zustandssumme, "sum over states" and is popularly known as partition function for canonical ensemble which is given by Z = 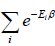
In systems with multiple quantum, we can write the partition function in terms of the
contribution from energy levels (indexed by i ) as follows:
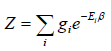
where gi is the degeneracy factor, or number of quantum states which have the same energy level defined by Ei .
In classical statistical mechanics, it is not really correct to express the partition function as a sum of discrete terms, as we have done.
In classical mechanics, the position and momentum variables of a particle can vary continuously, so the set of microstates is actually uncountable. In this case we must describe the partition function using an integral rather than a sum. For instance, the partition function of a gas of N identical classical particles is

Where pi indicate particle momenta xi indicate particle positions
d3 is a shorthand notation serving as a reminder that the pi and xi are vectors in three
dimensional space, and H is the classical Hamiltonian.
The reason for the ( N factorial): However, there is a well-known exception to this rule. If the sub-systems are actually identical particles, in the quantum mechanical sense that they are impossible to distinguish even in principle, the total partition function must be divided by a N! ( N factorial). For simplicity, we will use the discrete form of the partition function in this article. Our results will apply equally well to the continuous form.
The extra constant factor introduced in the denominator was introduced because, unlike the discrete form, the continuous form shown above is not dimensionless. To make it into a dimensionless quantity, we must divide it by where h is some quantity with units of action (usually taken to be Planck's constant).
Relation Between Macroscopic Variable and Canonical Partition Function Z
- Relation between total energy and partition function for large no for particle average of total energy E is equivalent to average of internal energy U .
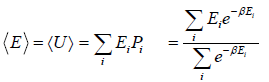 ∴
∴ 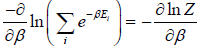
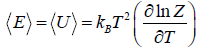 ⇒
⇒ 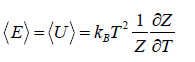
- Relation between partition function and specific heat at constant volume Cv
- Relation between partition function and Helmholtz free Energy:
 and
and  ,
,  =
= 
equating the coefficient of T 2 between relation
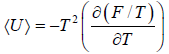 and so
and so 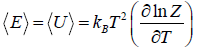 so F = - kBT InZ
so F = - kBT InZ
- relation between partition function and other thermodynamical variable once internal energy (U ) and Helmholtz free energy ( F ) is obtained one can find
(a) entropy ( S ) S = 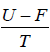
(b) pressure ( P ) P = 
(c) enthalpy( H ) H = U + PV
(d) Gibbs free energy G = H -TS
Relation Between Entropy and Probability
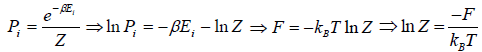

S = - 
Example 5: A system in thermal equilibrium has energies 0 and E. Calculate partition function of system.
Then calculate
(i) Helmholtz Free energy ( F )
(ii) entropy ( S )
(iii) internal energy (U )
(iv) Specific heat at constant volume Cv discuss the trend of specific heat at (a) low
temperature and (b) high temperature
Let T be the temperature of the system. The partition function Z of the system is
(i) Free energy F of the system is
(ii) Entropy S of the system is
S =
=
(iii) Internal energy U is
U = F + ST =
(iv) Specific heat at constant volume Cv is
Cv =
(a) At a low temperature
, and equation (3.35) reduces to
Cv =
Since with the decrease of T
Cv → 0, when T→ 0
(b) At a high temperature
and equation reduces to
Cv =
Hence, Cv → 0, when T → ∞
One Dimensional Free Particle
Example 6: The Hamiltonian of one dimensional N free particle is confine in box of length L given by E(q,p) =  write down
write down
(a) Expression of partition function
(b) Internal energy of system
(c) Specific heat at constant volume
ZN =
=
For evaluation of the first integral of equation let us put
= u and
= du
Using equations in the first integral equation we have
=
=
and integration of second integral is L
Partition function of one particle is Z =
Partition function of N particle is ZN =
(b) the internal energy (E) = (U) =
(E) = (U) =
(c)
Classical Harmonic Oscillator
Total energy of the system of N one dimensional classical oscillators is given by
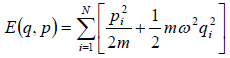
(a) Write down partition
(b) Helmholtz Free energy
(c) Internal energy
(d) Specific heat at constant volume
The partition function of the system is where
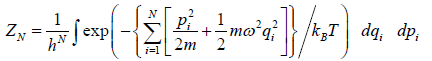
= 
For evaluation of the first integral of equation let us put 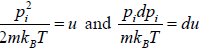
Using equations in the first integral equation we have
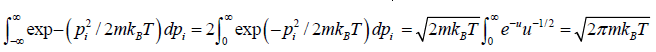
For evaluation of the second integral of equation, let us put
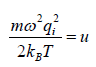 and
and 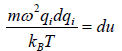
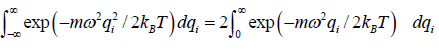
= 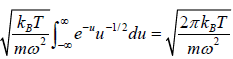
(a) Free energy F of the system is
F = 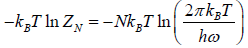
Once the free energy of the system is known, we can calculate other thermo dynamical quantities of the system.
(b) Entropy S of the system is

(c) Internal energy U is
U = 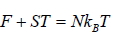
Thus, the mean energy per oscillator is kBT.
(d) Specific heat at constant volume Cv is
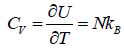 The specific heat at constant volume CV is independent of the temperature
The specific heat at constant volume CV is independent of the temperature
Quantum Harmonic Oscillator
Example 7: In quantum mechanics, energy of an oscillator is quantized and the energy of the N such system is given by

where ni is an integer ni = 0,1,2,3..; then find
(a) The partition function of the system
(b) Entropy
(c) Helmholtz free energy
(d) Internal energy
(e) Specific heat at constant volume, also discuss the case for lower temperature and higher temperature.
(a) 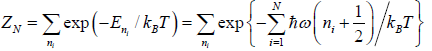
= 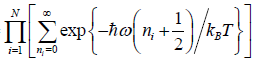
We know that 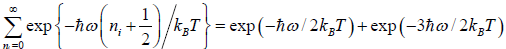 ....
....
= 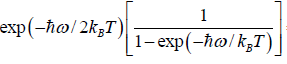 =
= 
Thus, the partition function is
ZN = 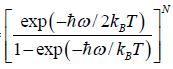
(b) Free energy F of the system is
F = 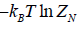 =
= 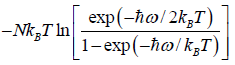
= 
Once the free energy of the system is known, we can calculate other thermodynamical quantities of the system.
(c) Entropy S of the system is
S = 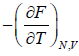 =
= 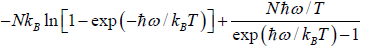
= 
(d) Internal energy U is U = F + ST = 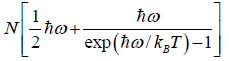
(e) Specific heat at constant volume Cv is
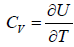 =
= 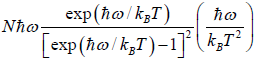 =
= 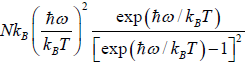
At a low temperature, we have 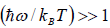 , and therefore, equation reduces to
, and therefore, equation reduces to
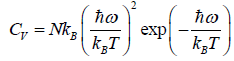
Since with the decrease of T, the function 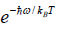 reduces much faster than the increase of the function
reduces much faster than the increase of the function 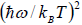 , therefore Cv → 0, when T→ 0
, therefore Cv → 0, when T→ 0
At a high temperature, we have 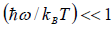 ,and therefore, equation reduces to
,and therefore, equation reduces to

It gives  when T→ ∞ it shows that the classical result for Cv is valid at high
when T→ ∞ it shows that the classical result for Cv is valid at high
temperature.
Example 7: In quantum mechanics, energy of an oscillator is quantized and the energy of the N such system is given by 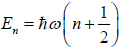 where n = 0,1,2,3,.... then
where n = 0,1,2,3,.... then
(a) Prove that partition function of the system is ZN = 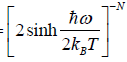
From the expression used in (a) then find
(a) Internal energy
(b) Specific heat at constant volume, also discuss the case for lower temperature and higher temperature.
(c) Helmholtz free energy
(d) Entropy.
(a) In quantum mechanics, the energy of an oscillator is
.
Thus, the quantum mechanical partition function for one oscillator is
=
Since, the partition function ZN of a system of N independent particles is equal to the
product of the partition function Z1 of individual particle, we have
(b) the internal energy U of the system is
U =
(c) Specific heat at constant volume Cv is
(d) The Helmohltz free energy F is
F =
(e) The entropy S is S =
Quantum Mechanical Treatment of Spin Half Paramagnetic Substance
Example 8: Suppose a system comprising identical particles is placed in a uniform magnetic field H and is kept at a temperature T . When a particle having spin 1/2 is placed in a magnetic field H , its each energy level splits into two with changes in energies by μH and the particle has a magnetic moment μ or -μ along the direction of the magnetic field, respectively. Find expressions for internal energy, entropy, specific heat and total magnetic moment M of this system with the help of the canonical distribution.
As the spins of particles are independent of each other, the partition function of the total system ZN is equal to the product of the partition functions for spins of individual particle. The partition function for spins of individual particle is
Thus,
The Helmholtz free energy is
F =
The entropy is
S =
Total energy is U = F + TS
Total magnetic moment is
The specific heat at constant volume CV is
Example 9: If Z is partition of one dimensional harmonic oscillator with energy 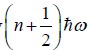 where n=0,1,2,3...at equilibrium temperature T.
where n=0,1,2,3...at equilibrium temperature T.
(a) what is probability that system has energy 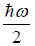
(b) what is probability that system has energy lower than 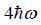
(c) what is probability that system has energy greater than 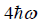
(a) If Z is partition of system what will be probability that system has energy
at equilibrium temperature T .
(b) System has smaller than energy
possible energy is
so
(c)
Example 10: A particle is confined to the region x ≥ 0 by a potential which increases linearly as
U(x) = u0x. find the mean position of the particle at temperature T .
Partition function is given by Z =
=
Grand canonical ensemble
In grand canonical ensemble, each element is in contact with reservoir where exchange of energy and particles is feasible. So in such type of ensemble energy (E) and number of particle (N) of system vary. This is an extension of the canonical but instead the grand canonical ensemble being modeled is allowed to exchange energy and particles with its environment. The chemical potential (μ) (or fugacity) is introduced to specify the fluctuation of the number of particles as chemical potential and particle numbers are thermodynamic conjugates. Popularly grand canonical ensemble is also known as T,V,μ .
Schematically the grand canonical ensemble can be represented as
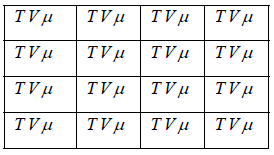
In above table each cell considers as each microstate temperature, volume and chemical potential which is fixed in each cell. Only value of energy and no of particle is different in different cell which can be exchanged in the process.
Grand canonical partition function is defined
In grand canonical ensemble for the system of interest having constant value of T,V,μ the partition function in classical system is given by
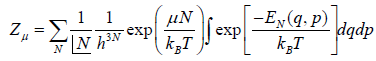
Where in quantum mechanical system 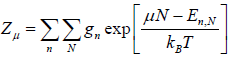
Thermo dynamical quantities in grand canonical ensemble
Relation between Helmholtz free energy and grand canonical partition function
According to Gibbs distribution function 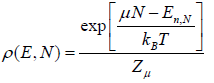
If ΔT is statistical weight which is equivalent to no of microstate Ω in micro canonical
ensemble then 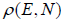 ΔT = 1 and ΔT =
ΔT = 1 and ΔT = 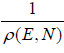
So entropy is given by S = 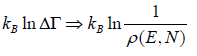
So entropy S = 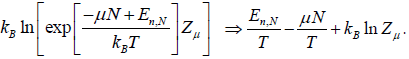
⇒ 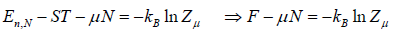
Where F - μN is popularly known as grand potential popularly represented by Ω.
⇒Ω = 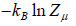
- Pressure of the system is P =
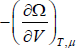
- The entropy of system is S=
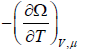
- The average number is N =

- Helmholtz free energy F =
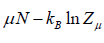
- Internal energy U = F + TS,
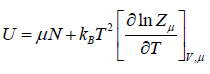
|
6 videos|20 docs|32 tests
|
FAQs on Basic Definition & Postulates of Statistical Mechanics - Kinetic Theory & Thermodynamics - Physics
| 1. What are the postulates of statistical mechanics? |  |
| 2. What is an ensemble in statistical mechanics? |  |
| 3. What is the canonical ensemble in statistical mechanics? |  |
| 4. What is the grand canonical ensemble in statistical mechanics? |  |
| 5. How is the grand canonical partition function defined? |  |