Basic Nuclear Properties: Assignment | Modern Physics PDF Download
Q.1. Assume that the nuclear binding energy per nucleon (B / A) versus mass number (A) is as shown in the figure. Use this plot and answer Yes or No for the given statement below.
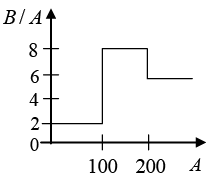
(a) Fusion of two nuclei with mass number lying in the range of 1 < A< 50 will release energy.
(b) Fusion of two nuclei with mass numbers lying in the range of 51 < A< 100 will release energy.
(c) Fission of a nucleus lying in the mass range of 100 < A< 200 will release energy when broken into two equal fragments.
(d) Fission of a nucleus lying in the mass range of 200 < A< 260 will release energy when broken into two equal fragments.
(a) If (BE)final - (BE)initial < 0 ; Energy will not be released. (No)
(b) If (BE)final - (BE)initial > 0 ; Energy will be released. (Yes)
(c) If (BE)final - (BE)initial < 0 ; Energy will not be released. (No)
(d) If (BE)final - (BE)initial > 0 ; Energy will be released. (Yes)
Q.2. (a) A stable nucleus has 1/3 the radius of 189Os nucleus. Find the stable nucleus.
(b) The radius of Ge nucleus is measured to be twice the radius of 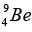 . How many nucleons are there in Ge nucleus?
. How many nucleons are there in Ge nucleus?
(c) Find approximately the ratio of the sizes of 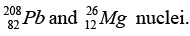
(d) The radius of a 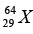 nucleus is measured to be 4.8 x10-13 cm. Find the radius of a
nucleus is measured to be 4.8 x10-13 cm. Find the radius of a 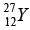 nucleus.
nucleus.
(b) ∵ R = R0 (A)1/3 and given that RGe = 2RBe ⇒R0 (AGe)1/3 = 2R0(9)1/3 ⇒ AGe = 72.
Q.3. Binding energy per nucleon vs. mass number curve for nuclei is shown in the figure. W , X , Y and Z are four nuclei indicated on the curve.
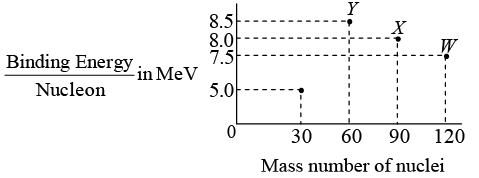
Check whether energy is released or absorbed in the process that are given below:
(a) Y → 2Z
(b) W → X + Z
(c) W → 2Y
(d) X → Y + Z
When total binding energy of products is more than that of reactants, energy is released in the process. Effectively the total binding energy is increased.
Total B.E. = B.E. per nucleon x number of nucleons
(a)
Reaction
Y → 2Z
Reactant
60 x 8.5 = 510 MeV
Product
2 x 30 x 5 = 300 MeV
Total binding energy is decreased, from 510 MeV to 300 MeV.
(b)
Reaction
W → X + Z
Reactant
120 x 7.5 = 900 MeV
Product
(90 x 8 + 30 x 5) = 870 MeV
Total binding energy is decreased, from 900 MeV to 870 MeV.
(c)
Reaction
W → 2Y
Reactant
120 x 7.5 = 900 MeV
Product
2 x 60 x 8.5 = 1020 MeV
Total binding energy is increased, in reaction W → 2Y from 900 MeV to 1020 MeV
(d)
Reaction
X → Y+ Z
Reactant
90 x 8 = 720 MeV
Product
(60 x 8.5 + 30 x 5) = 660 MeV
Total binding energy is decreased, from 720 MeV to 600 MeV.
Q.4. An alpha particle of energy 5 MeV is scattered through 180o by a fixed uranium nucleus. Find the distance of closest approach.
Energy is conserved.
Loss in kinetic energy = Gain in potential energy
The distance of closest approach is of the order of 10-12cm
Q.5. The atomic masses of 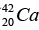 = 41.958622 u ,
= 41.958622 u ,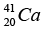 = 40.962278 u,
= 40.962278 u, 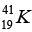 = 40.961825u and mass of
= 40.961825u and mass of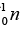 = 1.008665u ,
= 1.008665u , 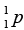 = 1.007276u.
= 1.007276u.
(a) Then the energy needed to remove a proton from the nucleus of the calcium isotope  energy needed to remove a neutron from the nucleus of the calcium isotope
energy needed to remove a neutron from the nucleus of the calcium isotope 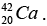
(b) Then the energy needed to remove a proton from the nucleus of the calcium isotope 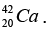
(a)
Total mass of the= 41.970943 u.
Mass defect Δm = 41.970943 - 41.958622 = 0.012321u
So, B.E. of missing neutron= Δm x 931.5 = 11.48 MeV
(b)
Total mass of the= 41.969101 u.
Mass defect Δm = 41.969101 - 41.958622 = 0.010479u
So, B.E. of missing proton = Δm x 931.5 = 10.27 MeV.
Q.6. In deep inelastic scattering electrons are scattered off protons to determine if a proton has any internal structure. Find the approximate energy of the electron.
The internal structure of proton can only be determined if the wavelength of the incoming electron is nearly equal to the size of the proton
i.e. λ = R = 1.2 A1/3 (fm) ≈ 1.2 fm = 1.2 x 10-15 m
According to de-Broglie relation,
This can be also written as
Q.7. The masses of a hydrogen atom, neutron and 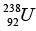 atom are given by 1.0078 u, 1.0087 u and 238.0508 u respectively.
atom are given by 1.0078 u, 1.0087 u and 238.0508 u respectively.
(a) Find the binding energy of 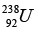 nucleus.
nucleus.
(b) Find the binding energy per nucleon of 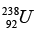 nucleus.
nucleus.
(a) B.E = [ZmH + Nmn - m (
)] x 931.5 MeV
⇒ B.E. = 92 x 1.0078 + 146 x 1.0087 - 238.0508] x 931.5 MeV
⇒ B.E. = 1.937 x 931.5 MeV = 1804 MeV
(b) B.E./A = 1804/238 = 7.6MeV/ nucleons
Q.8. A nucleus has a size of 10-15 m. Consider an electron bound within a nucleus. Estimated the energy of this electron.
= 1.5 x 1012 MeV = 1.5 x 106 MeV = 150 x 104 MeV
Q.9. The measured mass of deuteron atom 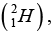 Hydrogen atom
Hydrogen atom 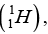 proton (p) and neutrons (n) are 2.0141 u, 1.0078 u, 1.0073 u and 1.0087 u.
proton (p) and neutrons (n) are 2.0141 u, 1.0078 u, 1.0073 u and 1.0087 u.
(a) Find the binding energy of the deuteron nucleus.
(b) Find the binding energy per nucleon of the deuteron nucleus.
⇒ B.E. = [1x1.0078 + 1x1.0087 - 2.0141] x 931.5 MeV
⇒ B.E. = 0.0024 x 931.5 MeV = 2.2356 MeV
(b) B.E/A = 2.2356/2 = 1.1178 MeV / nucleons
Q.10. The electrostatic energy of Z protons uniformly distributed throughout a spherical nucleus of radius R is given by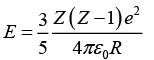
The measured mass of the neutron, 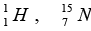 and
and 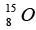 are 1.008665 u , 1.007825 u ,15.000109u and 15.003065 u respectively. Given that the radii of both the
are 1.008665 u , 1.007825 u ,15.000109u and 15.003065 u respectively. Given that the radii of both the 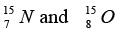 nuclei are same. 1u = 931.5MeV / c2 (c is the speed of light) and e2 / (4πε0) = 1.44 MeV fm. Assuming that the difference between the binding energies of
nuclei are same. 1u = 931.5MeV / c2 (c is the speed of light) and e2 / (4πε0) = 1.44 MeV fm. Assuming that the difference between the binding energies of 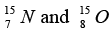 is purely due to the electrostatic energy, find the radius of either of the nuclei. (1fm = 10-15m)
is purely due to the electrostatic energy, find the radius of either of the nuclei. (1fm = 10-15m)
and
Now mass defect of N atom = 7 x 1.007825 + 8 x 1.008665 - 15.000109 = 0.1239864 u
So, binding energy = 0.1239864 x 931.5 MeV
And mass defect of O atom = 8 x 1.007825 + 7 x 1.008665 -15.003065 = 0.12019044 u
So binding energy = 0.1239864´ 931.5 MeV
So |B0 - BN| 0.0037960x931.5 MeV ......(ii)
From (i) and (ii) we get
R = 3.42 fm
|
37 videos|16 docs|19 tests
|
FAQs on Basic Nuclear Properties: Assignment - Modern Physics
| 1. What are the basic nuclear properties? |  |
| 2. How is atomic number related to the number of protons? |  |
| 3. What is the significance of isotopes? |  |
| 4. How does nuclear stability affect the behavior of atoms? |  |
| 5. What is nuclear decay and how does it occur? |  |

|
Explore Courses for Physics exam
|

|







 = 41.970943 u.
= 41.970943 u.
 = 41.969101 u.
= 41.969101 u.


 )] x 931.5 MeV
)] x 931.5 MeV























