Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Basic Probability
Basic Probability | Mathematics for GCSE/IGCSE - Class 10 PDF Download
Basic Probability
What is probability?
- Definition: Probability refers to the likelihood of an event occurring.
- In Real Life: In everyday scenarios, we use terms like impossible, unlikely, or certain to express probabilities.
- Probability Scale: Mathematically, probabilities are represented on a scale from 0 (impossible) to 1 (certain).
- Representation: Probabilities can be conveyed as fractions, decimals, or percentages.
What key words and terminology are used with probability?
- An experiment is a task that can be done repeatedly, producing observable or recordable results.
- Trials are the individual repetitions of an experiment.
- An outcome refers to any possible result of a single trial.
- An event is either a single outcome or a group of outcomes.
- Events are typically labeled with capital letters like A, B, etc.
- n(A) represents the number of outcomes belonging to event A.
- Events can comprise one or multiple outcomes.
- The sample space is the complete set of all potential outcomes from an experiment, often depicted as a list or a table.
- The probability of event A is symbolized as P(A).
How do I calculate basic probabilities?
- If all outcomes have an equal chance of occurring, then each outcome has the same probability.
- The probability for each outcome is
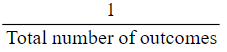
- For instance, if there are 50 marbles in a bag, the probability of selecting a specific marble is 1/50.
- The probability for each outcome is
- The theoretical probability of an event can be determined without conducting an experiment by dividing the number of outcomes favorable to the event by the total number of outcomes.
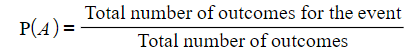
- For example, if there are 50 marbles in a bag and 20 of them are blue, then the probability of selecting a blue marble is 20/50.
- Sometimes, listing or tabulating all possible outcomes can aid in identifying them in certain situations.
How do I find missing probabilities?
- The sum of the probabilities of all outcomes in an experiment equals 1.
- If you have a probability table with one probability missing, you can find it by subtracting the sum of the other probabilities from 1.
- The complement of event A represents the event where A does not occur, often denoted as A'.
- This can be conceptualized as the opposite of A.
- Mathematically, it's represented as P(A) + P(A') = 1.
- This is commonly expressed as P(A') = 1 - P(A).
What are mutually exclusive events?
- Two events are mutually exclusive if they cannot both occur simultaneously.
- For instance, in rolling a die, the events "rolling a prime number" and "rolling a 6" are mutually exclusive.
- If events A and B are mutually exclusive, then to calculate the probability of either A or B occurring, you can just add the probabilities of A and B together.
- Complementary events are also mutually exclusive.
Possibility Diagrams
What is a possibility diagram (sample space)?
- In probability, the sample space refers to all the potential outcomes.
- In simple scenarios, the sample space can be presented as a list.
- For instance, when flipping a coin, the sample space includes "Heads" and "Tails," often abbreviated as H and T.
- Similarly, for rolling a six-sided die, the sample space comprises the numbers 1 through 6.
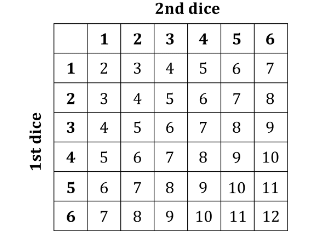
- When dealing with combined events, such as rolling two dice and adding their scores, a grid or possibility diagram can be utilized.
- A comprehensive list of all possibilities would be lengthy and prone to omissions.
- Identifying missed possibilities or patterns in the sample space would be challenging with a long list.
- Therefore, using a possibility diagram is preferable for clarity and ease of analysis.
- If you need to combine more than two things you'll probably need to go back to listing
- For example, flipping three coins (or flipping one coin three times!)
- In this case the sample space is: HHH, HHT, HTH, THH, HTT, THT, TTH, TTT (8 possible outcomes)
- For example, flipping three coins (or flipping one coin three times!)
How do I use a possibility diagram to calculate probabilities?
Probabilities can be determined by counting desired outcomes and dividing by the total possibilities in the sample space.
Basic Concept of Probabilities:
- In a sample space like 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, where 4 numbers (2, 3, 5, and 7) are prime, the probability of selecting a prime number is calculated as the number of prime numbers divided by the total numbers in the sample space.
- When rolling two dice and summing the results, for instance, to find the probability of getting an 8, we can observe that there are 5 ways to achieve this outcome out of 36 total possibilities.
Consideration of Fairness:
- It's essential to note that this counting method works effectively when all outcomes in the sample space are equally likely. For example, in a fair six-sided die, each number (1, 2, 3, 4, 5, 6) has an equal likelihood of occurring.
- Similarly, in the case of a fair coin with outcomes 'H' (Heads) and 'T' (Tails), both are equally likely.
- However, when it comes to winning the lottery, the outcomes 'Yes' and 'No' are not equally likely, so the simple counting method cannot be applied here.
Conditional Probability:
- Conditional probability involves finding the likelihood of an event given that another event has occurred. For example, when rolling two dice, we can calculate the probability of one die showing a 6, given that the total sum on both dice is 7.
- To achieve this, we count the total outcomes that sum to 7 (6 outcomes) as the denominator.
- Among these, we count the outcomes where one die shows a 6 (2 outcomes: (1, 6) and (6, 1)) as the numerator to find the conditional probability.
- So the probability is 2/6 = (1/3)
Question for Basic ProbabilityTry yourself:What is the probability of rolling a prime number on a fair six-sided die?
View Solution
The document Basic Probability | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
66 videos|674 docs|19 tests
|
FAQs on Basic Probability - Mathematics for GCSE/IGCSE - Class 10
| 1. What is a possibility diagram in basic probability? |  |
Ans. A possibility diagram, also known as a sample space diagram, is a visual representation of all possible outcomes of a random experiment in probability theory.
| 2. How is a possibility diagram used in basic probability? |  |
Ans. A possibility diagram helps in visualizing all possible outcomes of an event, making it easier to calculate probabilities and analyze the likelihood of different outcomes.
| 3. What is the importance of understanding basic probability in mathematics? |  |
Ans. Understanding basic probability is crucial in mathematics as it helps in making informed decisions, predicting outcomes, and analyzing uncertainties in various real-life scenarios.
| 4. How can one calculate probabilities using a possibility diagram? |  |
Ans. To calculate probabilities using a possibility diagram, one can count the number of favorable outcomes and divide it by the total number of possible outcomes in the sample space.
| 5. Can possibility diagrams be used in more complex probability problems? |  |
Ans. Yes, possibility diagrams can be used in more complex probability problems by expanding the sample space to include all possible outcomes and analyzing the probabilities of different events accordingly.
Related Searches
















